Представление информации в ЭВМ

Наиболее удобным средством представления информации, с точки зрения автоматизации процессов ее обработки, является язык чисел. Любой язык чисел определяется системой счисления. Система счисления – способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения.

Различают непозиционные и позиционные системы счисления. В непозиционной системе счисления цифры не меняют своего количественного значения при изменении их расположения в числе. Тем самым исключается всякая возможность автоматизации распознавания чисел и, как следствие, обработки информации. Этого недостатка лишена позиционная система счисления, в которой значение каждой цифры зависит от ее места (позиции) в числе. Позиционные системы счисления характеризуются:

· основанием Р системы счисления –количеством (Р) различных символов, используемых для изображения чисел. Значения этих символов лежат в пределах от 0 до Р-1;

· разрядом – позицией,занимаемой отдельным символом в изображении числа. Разряды нумеруются справа налево, начиная с 0;

· весом разряда –количественным значением одной единицы разряда. Численно вес разряда определяется через основание Р системы счисления и номер i разряда: Рi.

Таким образом, максимальное целое число, которое может быть представлено в m разрядах – Nmax = Pm -1. Минимальное значащее (не равное 0) число, которое можно записать в s разрядах дробной части – Nmin = P-s. Тогда, имея в целой части числа m, а в дробной s разрядов, можно представить Pm+s чисел от 0 до Pm+s -1.

Поскольку в технике известно много физических приборов и сред с двумя устойчивыми состояниями, в качестве алфавита языка ЭВМ приняты символы 0 и 1, названные двоичными цифрами. Последовательности нулей и единиц конечной длины образуют двоичные числа, которые, в свою очередь, образуют позиционную двоичную систему счисления.

В вычислительных машинах применяются две формы представления двоичных чисел – естественная форма или форма с фиксированной запятой (точкой) и нормальная форма или форма с плавающей запятой (точкой).

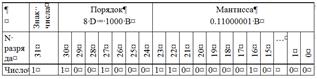
В естественной форме положение в разрядной сетке (общее число разрядов, отведенное для представления чисел, с указанием местоположения каждого из них) запятой, отделяющей целую часть числа от дробной части, постоянно для всех чисел.

Рис. 4.1

Машинное словоявляется структурной единицей информации ЭВМ. С помощью машинного слова записываются числа, символы и команды.

В современных ЭВМ длина машинных слов составляет 32 . . . 128 разрядов На рисунке 1 для упрощения показано слово длиной 16 разрядов (2 байта). Физически каждый разряд машинного слова представляет собой отдельный элемент памяти (триггер или запоминающий конденсатор).

Диапазон значащих чисел небольшой и при m-разрядной целой части и s-разрядной дробной части числа без учета знака составляет от P^-s до P^m - P^-s. Кроме того, если в результате операции получится число, выходящее за допустимый диапазон, происходит переполнение разрядной сетки, и дальнейшие вычисления теряют смысл. Следовательно, необходимо прогнозировать результаты обработки с целью соответствующего масштабирования исходных данных. По этим причинам естественная форма представления используется как вспомогательная и только для целых чисел.

В нормальной форме каждое число представляется как N = ±MP^±R, где М – мантисса числа (|M|<1), R – порядок (целое число), Р – основание системы счисления. Абсолютное значение порядка определяет число разрядов, на которое смещена запятая, отделяющая целую часть числа от дробной части, а знак порядка – направление смещения этой запятой. Таким образом, с изменением значения порядка запятая меняет своё положение, как бы «плавает» в изображении числа. Диапазон значащих чисел весьма велик и при m-разрядной мантиссе и s-разрядном порядке (без учета знаков порядка и мантиссы) составляет от 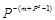до (1- P^-m) 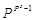. В связи с этим нормальная форма представления является основной в современных ЭВМ.

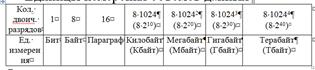
В соответствии с двоичным представлением в информатике введены специальные единицы измерения объемов информации, хранимой или обрабатываемой в ЭВМ (таблице 4.1).

Последовательность нескольких битов или байтов часто называют полем данных. В ПК могут обрабатываться поля постоянной и переменной длины.

Таблица4.1. Единицы измерения объемов данных

Поля постоянной длины могут быть следующих размеров (форматов):

· слово — 2 байта

· двойное слово — 4 байта

· полуслово — 1 байт

· расширенное слово — 8 байт

· слово длиной 10 байт — 10 байт

В полях постоянной длины числа с фиксированной запятой чаще всего имеют формат слова (рис.4.2 а) и полуслова и заполняют формат справа налево. Оставшиеся свободными старшие разряды формата заполняются нулями. В крайнем левом разряде формата отображается знак числа, при этом знак «+» кодируется нулем, а знак «-» – единицей.

Числа с плавающей запятой чаще всего имеют формат двойного (рис. 4.2б) и расширенного слова. Порядок заполняет соответствующую часть формата справа налево, а мантисса – слева направо. Оставшиеся свободными младшие разряды мантиссы формата заполняются нулями.

Поля переменной длины могут иметь любой размер от 0 до 256 байт, но обязательно равный целому числу байтов.

Рис. 4.2 Структура формата слово со знаком для чисел с фиксированной (а) и плавающей (б) запятой

Пример 1. Структурно запись числа -193(10) = -11000001(2) в разрядной сетке ПК выглядит следующим образом.

Число с фиксированной запятой формата слово со знаком:

Числа с плавающей запятой Под знак и порядок отводится старший байт числа. Для возможности представления как положительного так и отрицательного порядка применяют смещенный порядок. То есть машинный порядок (Мр) представляют со смещением на 64. ( Мр=Р+64. ). Таким образом при машинном порядке равном нулю (0000000 В) реальный порядок равен -64, а при максимальном машинном порядке (1111111 В) равном 127, порядок равен +63.

Число с плавающей запятой формата двойное слово: -193(10) = -11000001(2) = -0.11000001*2⁸. Здесь мантисса = -0.11000001, а порядок =1000(2).

Машинный порядок Мр=1000000(2)+ 1000(2) = 1001000(2).

При выполнении операций ввода-вывода данные часто представляются в двоично-десятичной системе счисления – когда каждая цифра десятичного числа отображается 4-разрядным двоичным числом. Двоично-десятичные числа представляются полями переменной длины в так называемых упакованном и распакованном форматах. В упакованном формате для каждой десятичной цифры отводится 4 двоичных разряда, при этом знак числа кодируется в крайнем правом полубайте (1100 – знак «+» и 1101 – знак «-»). Упакованный формат используется обычно в ПК при выполнении арифметических операций над двоично-десятичными числами. В распакованном формате для каждой десятичной цифры отводится байт, представляющий собой (кроме младшего байта) адрес соответствующей ячейки таблицы символов. В старшем полубайте адреса кодируется номер столбца, а в младшем – номер строки этой таблицы. Старший полубайт младшего (правого) байта используется для кодирования знака. Распакованный формат используется в ПК при вводе-выводе информации.

Двоично-десятичные кодированные числа могут быть представлены в ПК полями переменной длины в так называемых упакованном и распакованном форматах.

В упакованном формате для каждой десятичной цифры отводится по 4 двоичных разряда (полбайта), при этом знак числа кодируется в крайнем правом полубайте числа (1100 — знак "+" и 1101 — знак "-").

Структура поля двоично-десятичного упакованного формата:

Здесь и далее: Цф — цифра. Знак — знак числа

Упакованный формат используется обычно в ПК при выполнении операций сложения и вычитания двоично-десятичных чисел.

В распакованном формате для каждой десятичной цифры отводится по целому байту, при этом старшие полубайты (зона) каждого байта (кроме самого младшего) в ПК заполняются кодом 0011 (в соответствии с ASCII-кодом), а в младших (левых) полубайтах обычным образом кодируются десятичные цифры. Старший полубайт (зона) самого младшего (правого) байта используется для кодирования знака числа.

Структура поля распакованного формата:

Распакованный формат используется в ПК при вводе-выводе информации в ПК, а также при выполнении операций умножения и деления двоично-десятичных чисел.

Пример 3.Число -193(10) = -000110010011 (2-ю) в ПК будет представлено:

в упакованном формате —

в распакованном формате —