Расчет симметричных многополюсников
При расчете матрицы рассеяния симметричных многополюсников, используя свойство симметрии, можно свести этот расчет к расчету матрицы рассеяния более простых многополюсников, составляющих данный. Если многополюсник обладает геометрической плоскостью симметрии, то можно сказать, что эта плоскость симметрии определяет и симметрию электрических характеристик многополюсника (элементов матрицы рассеяния) обратное не всегда справедливо. Рассмотрим симметричный четырехполюсник
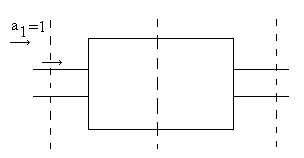
Такое возбуждение линейного четырехполюсника – результат сложения симфазного и противофазного возбуждения данного четырехполюсника.
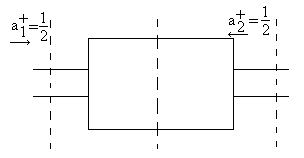 a) Симфазное возбуждение (XX)
a) Симфазное возбуждение (XX)
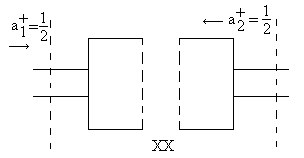
 b) Противофазное возбуждение (КЗ)
b) Противофазное возбуждение (КЗ)
В плоскости симметрии – пучность U. Но пучность характерна для режима ХХ, т. е. в случае а) имеем в плоскости симметрии ХХ.
В случае b) в плоскости симметрии имеем узел напряжения – режим КЗ. Тогда

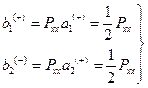 Симфазное возбуждение
Симфазное возбуждение
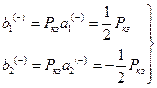 Противофазное возбуждение
Противофазное возбуждение
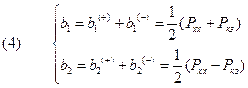


т. к. симметричный четырехполюсник
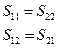
сопоставим (3) и (4)
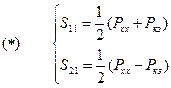
Расчет элементов матрицы мы свели к расчету коэффициентов отражения на входах составляющих двухполюсников в режиме ХХ и КЗ.
Пример 1
Рассчитать матрицу рассеяния четырехполюсника в виде отрезка двухпроводной линии
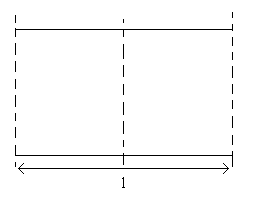
Используем метод зеркальных изображений, вводя плоскость симметрии.
Выделим двухполюсник в режиме ХХ и КЗ.

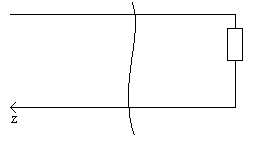
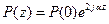
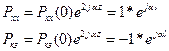
Воспользуемся (*)

Пример 2
Вычислить матрицу рассеяния, для двухпроводной линии с параллельным сопротивлением.
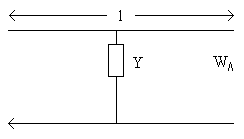
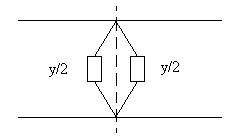
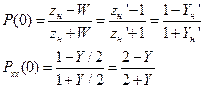
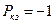
Тогда
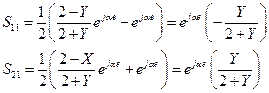
Изменим плоскости отсчета, чтобы компенсировать фазы элементов матрицы расчета
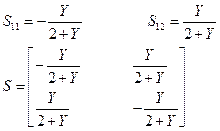
Дата добавления: 2015-04-21; просмотров: 1302;
