Основные положения теории подобия

В основе методов моделирования лежит учение о подобии, основы которого заложены еще И. Ньютоном.

Некоторые две системы А и А₁ подобны в том случае, если параметры этих систем удовлетворяют общему дифференциальному уравнению связи, выражающему критерий термодинамического подобия. Признаки подобия рассматриваемых явлений между собой характеризуются тремя теоремами подобия.

Первая теорема подобия, установленная Ж. Бертраном (1848), основана на общем понятии динамического подобия и втором законе механики Ньютона. Акад. М.В. Кирпичев дает следующую формулировку первой теоремы подобия: подобными называют явления, происходящие в геометрически подобных системах, если у них во всех сходственных точках отношения одноименных величин есть постоянные числа.

Вторая теорема подобия, сформулированная в начале XX в. независимо друг от друга А. Федерманом и Дж. Букингемом, устанавливает возможность такого преобразования физического уравнения связи, описывающего данное явление, при котором получают уравнение, составленное из критериев (или инвариантов) подобия. Иначе говоря, согласно второй теореме результаты опытов по изучению какого-либо физического явления, представленные в виде критериальных уравнений связи, возможно перенести на другие явления, подобные исследованному в опыте.

Третья теорема подобия, называемая теоремой о существовании подобия, сформулирована и доказана акад. М.В. Кирпиче-вым (1930). Согласно этой теореме для существования подобия между явлениями необходимо и достаточно, чтобы эти явления имели подобные условия однозначности и одинаковые определяющие критерии подобия.

Условия однозначности — это условия, в соответствии с которыми из всей совокупности однотипных явлений выделяют одно конкретное явление. Подобие условий однозначности устанавливают по следующим признакам:

а) подобию геометрических свойств систем;

б) пропорциональности физических констант, имеющих существенное значение в изучаемом процессе;

в) подобию начального состояния систем;

г) подобию условий на границах систем в течение всего рассматриваемого периода процесса;

д) равенству определяющих критериев, при этом определяющими критериями подобия являются те, которые составлены из величин, входящих в условия однозначности, т. е. имеющих существенное значение в изучаемом процессе.

Применение методов моделирования при решении задач геомеханики позволяет изучать на моделях действие механических силовых полей в деформируемых массивах горных пород вокруг выработок, т. е. породные массивы и их модели являются механически подобными системами. Для установления необходимых критериев и констант подобия таких систем должен быть использован закон динамического подобия Ньютона наряду с применением метода размерностей.

При характеристике того или иного механического процесса механическое подобие может быть определено заданием переходных множителей или масштабов для длин (геометрическое подобие), времени (кинематическое подобие) и масс (динамическое подобие).

Для двух подобных систем условие геометрического подобия состоит в том, что все размеры пространства, занятого системой в модели, и размеры отдельных элементов модели изменены в определенное число mi раз по сравнению с соответствующими размерами натуры:

L_M /L_H= m_L, (12.1)

где L_M и L„ — соответственно линейные размеры модели и натуры.

Условие кинематического подобия этих систем состоит в том, что любые сходственные точки (частицы) систем, двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути в промежутки времени Т, отличающиеся постоянным множителем т_т:

Т_м/Т_И=т_т. (12.2)

Условие динамического подобия систем состоит в том, что массы любых сходственных частиц этих систем отличаются друг от друга постоянным множителем т^:

М_м/М_н= т_м- (12.3)

Если в формуле (12.3) выразить массу как произведение объема частицы на ее плотность, то условие динамического подобия достаточно задать отношением плотностей:

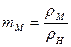. (12.4)

Применяя теорию размерностей и имея значения трех основных переходных множителей m_L, m_T и т_м, можно выразить отношение любых элементов подобных систем.

В частности, в условиях действия гравитационных сил условие динамического подобия (критерий Ньютона) выражается соотношением

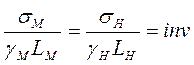(12.5)

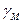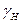где и — объемный вес соответственно материала в модели и породы в натуре; 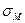и 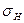— напряжения соответственно в материале модели и в породе натуры.

Анализ выражения (12.5) показывает, что при заданном геометрическом масштабе моделирования ( 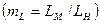для обеспечения механического подобия модели и натуры необходимо отказаться в модели либо от равенства γ_м = γ_н, либо от равенства обоих показателей.

Если сохранить в модели равенство механических свойств материала модели и натуры, т. е. условие 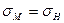, то необходимо, чтобы объемный вес материала модели удовлетворял условию

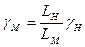(12.6)

Иначе говоря, применив в модели материал, имеющий одинаковые механические свойства с горными породами натуры, для выполнения условий механического подобия требуется увеличить, объемный вес материала в число раз, обратное геометрическому масштабу моделирования.

Например, при геометрическом масштабе модели 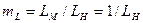объемный вес материала модели должен быть равен

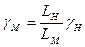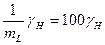= (12.7)

Условие (12.7) можно выполнить, применив в модели натуральные горные породы и придав им фиктивный объемный вес (100γ_н в приведенном случае при 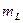= 1/100) с помощью инерционных сил, которые могут быть созданы, например, путем вращения модели в центрифуге при соответствующем значении центробежной силы. Этот метод был предложен в 1932 г. профессорами Г.И. Покровским и Н.Н. Давиденковым и носит название метода центробежного моделирования.

Если же в модели применить некоторые искусственные материалы, механические характеристики которых ниже соответствующих характеристик моделируемых горных пород, т. е. отказаться от равенства 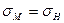, то для обеспечения условий механического подобия модели и натуры необходимо

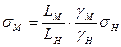(12.8)

Искусственные материалы, соответствующие механические характеристики которых в принятом геометрическом масштабе моделирования удовлетворяют по отношению к моделируемым горным породам условию (12.8), называют материалами — эквивалентами данным горным породам или эквивалентными материалами. Метод моделирования, основанный на применении эквивалентных материалов и предложенный в 1936 г. проф. Г.Н. Кузнецовым, носит название метода эквивалентных материалов.