Последовательное соединение r, L, C
Допустим, имеется цепь с последовательно соединенными элементами r, L, C (рис. 3.11) по которой протекает синусоидальный ток:
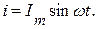
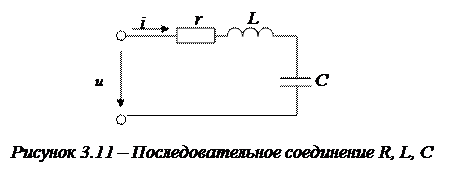
Согласно второму закону Кирхгофа:
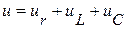 .
.
Соотношения между величинами действующих значений напряжений на элементах цепи, можно оценить с помощью векторной диаграммы (рис. 3. 12).
Порядок построения векторной диаграммы следующий.
1. Откладываем вектор тока I в произвольном направлении.
2. Откладываем падение напряжения на всех элементах:
2.1. Напряжение на резистивном элементе 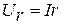 совпадает по направление с током
совпадает по направление с током 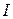 .
.
2.2. Напряжение на индуктивном элементе 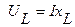 опережает по направлению ток
опережает по направлению ток 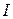 на 900.
на 900.
2.3. Напряжение на емкостном элементе 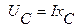 отстает по направлению от тока
отстает по направлению от тока 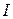 на 900.
на 900.
3. Вектор напряжения 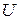 на зажимах цепи, получаем путем векторного сложения
на зажимах цепи, получаем путем векторного сложения 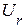 ,
, 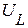 ,
, 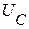 (начало вектора
(начало вектора 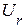 соединяем с концом вектора
соединяем с концом вектора 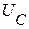 ).
).
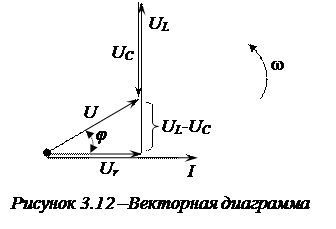 |
Из векторной диаграммы следует:
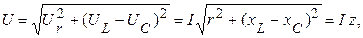
где 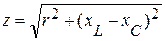 –полное сопротивление цепи.
–полное сопротивление цепи.
Выражение 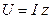 называют законом Ома для цепи синусоидального тока.
называют законом Ома для цепи синусоидального тока.
Угол jпоказывает сдвиг по фазе между напряжением и током на зажимах.
В приведенном примере напряжение опережает ток на j, т.к. xL > xCи режим работы цепи активно-индуктивный.
При xL < xC, ток опережает напряжение на jи режим работы активно-емкостной.
При xL = xC, ток совпадает с напряжением по фазе. В этом случае 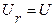 , режим работы активный. В цепи имеет место резонанс.
, режим работы активный. В цепи имеет место резонанс.
Соотношения между величинами активного 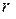 , реактивного
, реактивного 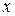 и полного
и полного 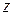 сопротивлений можно оценить с помощью треугольника сопротивлений (рис. 3.13).
сопротивлений можно оценить с помощью треугольника сопротивлений (рис. 3.13).
Реактивное сопротивление x = xL - xC.
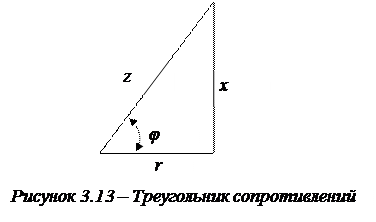 |
Из этого треугольника следует: 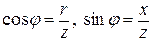 .
.
Свойства последовательно соединённых элементов
Рассмотрим пример электрической цепи, приведенный на рисунке 3.14, состоящей из разнородных элементов (четырех резистивных элементов - 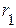 ,
, 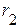 ,
, 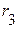 ,
, 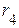 , трех индуктивностей -
, трех индуктивностей - 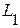 ,
, 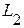 ,
, 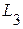 и двух емкостей -
и двух емкостей - 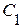 ,
, 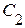 ), соединенных последовательно.
), соединенных последовательно.
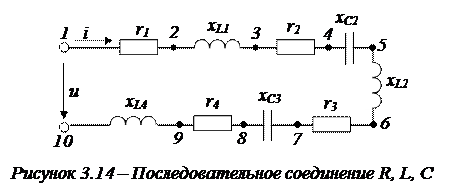 |
Вычертим векторную диаграмму этой цепи (рис. 3.15).
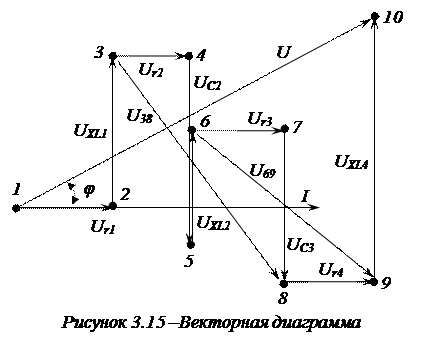
Вектор тока откладываем в произвольном направлении. Далее откладываем падение напряжения на всех элементах: напряжения и ток на резистивных элементах совпадают по фазе, напряжение на индуктивных элементах по фазе опережает ток на 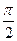 , ток на емкостных элементах опережает напряжение на
, ток на емкостных элементах опережает напряжение на 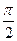 .
.
Используя векторную диаграмму можно определить величину напряжения на любом участке электрической цепи и его сдвиг по фазе относительно тока. Например, напряжение между точками схемы 3 и 8 равно - 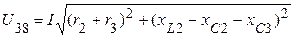 , а между точками 6 и 9 -
, а между точками 6 и 9 - 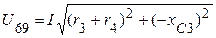 .
.
В общем случае суммарное падение напряжения на резистивных элементах равно 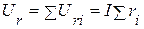 , на индуктивных элементах -
, на индуктивных элементах - 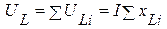 ,на емкостных элементах -
,на емкостных элементах - 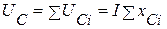 . Таким образом, последовательно соединённые резистивные, индуктивные и емкостные можно заменить эквивалентными. Они соответственно равны:
. Таким образом, последовательно соединённые резистивные, индуктивные и емкостные можно заменить эквивалентными. Они соответственно равны:
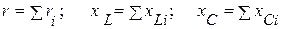 .
.
Тогда полное сопротивление всей ветви, соответственно равно:
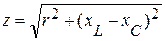
При последовательном соединении резистивного, индуктивного и емкостного элементов, напряжение на зажимах цепи, можно разбить на две составляющие напряжения активную 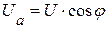 и реактивную
и реактивную 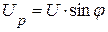 (рис. 3.16).
(рис. 3.16).
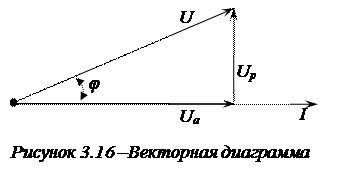 |
Из приведенной векторной диаграммы следует: 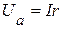 ,
, 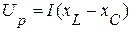 .
.
Пример 3.1. Возможные варианты расчета цепей с последовательным соединением, рассмотрим на примере электрической цепи, представленной на рисунке 3.17. Заданы величины U = 170 (B), ω = 314 (рад/с) (f = 50 Гц), r1 = 10 (Ом), r2 = 9 (Ом), r3 = 14 (Ом), L1 = 30 (мГн), С2 = 90 (мкФ), L3 = 25 (мГн). Необходимо определить ток в цепи, напряжения на элементах цепи и напряжение на участке 3-6.
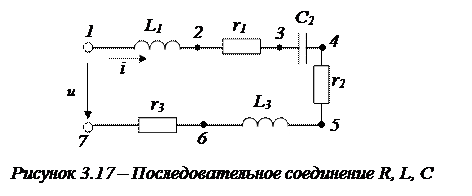 |
1. Определяем омические сопротивления реактивных элементов:
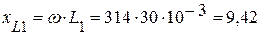 (Ом),
(Ом),
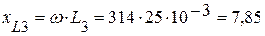 (Ом),
(Ом),
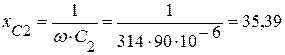 (Ом).
(Ом).
2. Определяем полное сопротивление ветви.
2.1. Эквивалентное активное сопротивление
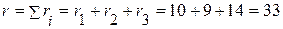 (Ом).
(Ом).
2.2. Эквивалентное индуктивное сопротивление
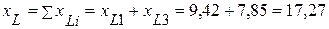 (Ом).
(Ом).
2.3. Эквивалентное емкостное сопротивление
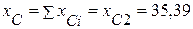 (Ом).
(Ом).
2.4. Полное сопротивление
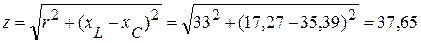 (Ом).
(Ом).
3. Определяем ток в цепи 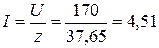 (А).
(А).
4. Определяем напряжения на каждом элементе цепи
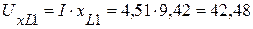 (В),
(В),
 (В),
(В),
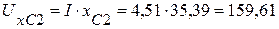 (В),
(В),
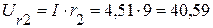 (В),
(В),
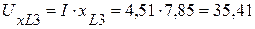 (В),
(В),
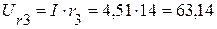 (В).
(В).
5. Напряжение на участке цепи 3-6 равно
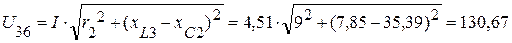 (В).
(В).
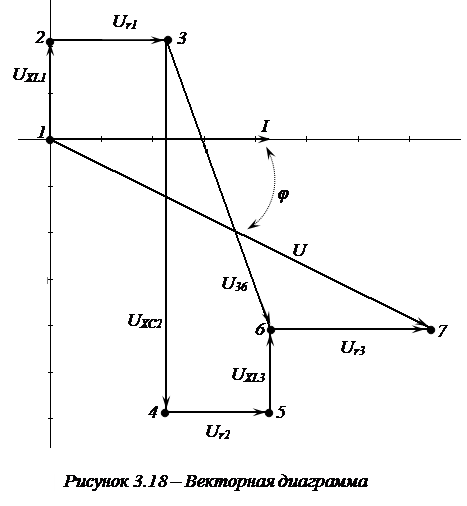
6. Векторная диаграмма рассматриваемой цепи приведена на рисун- ке 3.18.
 |
Дата добавления: 2015-04-21; просмотров: 13424;
