Обращение простых интервалов
Обращением интервала называется результат перемены мест составляющих его тонов, когда основание становится вершиной, а вершина — основанием интервала.
При обращении обязательно образуется новый интервал, который вместе с первоначальным непременно составляет октаву. Однако числовое выражение суммы обоих интервалов (данного и его обращения) всегда будет равняться 9 (а не 8), так как во взаимообратимых интервалах один из звуков считается дважды, ибо входит как в первый, так и во второй интервал. Итак:
| прима | обращается в | октаву | (1 + 8 = 9) | квинта | — »— | кварту | (5 + 4 = 9) | |
| секунда | — »— | септиму | (2 + 7 = 9) | секста | — »— | терцию | (6 + 3 = 9) | |
| терция | — »— | сексту | (3 + 6 = 9) | септима | — »— | секунду | (7 + 2 = 9) | |
| кварта | — »— | квинту | (4 + 5 = 9) | октава | — »— | приму | (8 + 1 = 9) |
Из приведенной таблицы видно, что тесные интервалы (от примы до кварты включительно) обращаются в широкие (от квинты до октавы включительно) и наоборот.
Сам процесс обращения простых интервалов сводится к следующему: один из звуков данного интервала переносится на октаву в сторону, противоположную его местонахождению (основание — вверх или вершина — вниз), а другой звук при этом остается на месте, в результате чего образуется новый интервал, являющийся обращением первого, где функции составляющих его звуков меняются ролями: основание становится вершиной, а вершина — основанием. Если подвергающийся переносу на октаву звук был альтерированным, то он сохраняет свой знак альтерации:
79 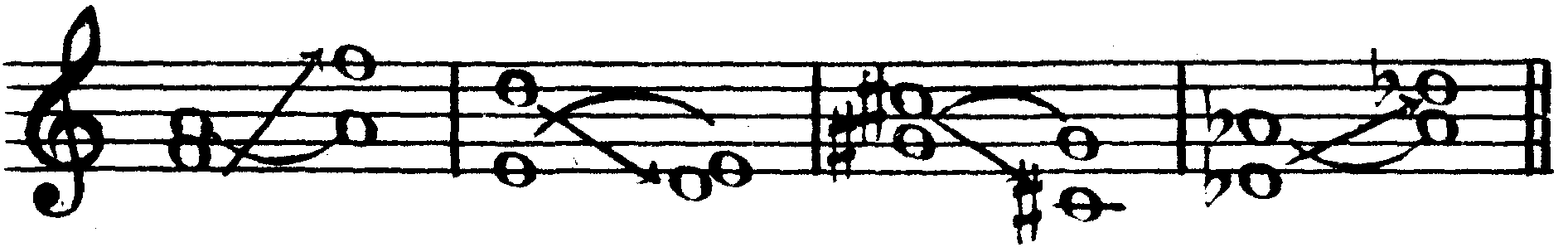
Что же касается вида интервала, определяемого, как известно, его тоновой величиной, то при обращении все интервалы (за исключением чистых) получают противоположный вид, то есть большие интервалы обращаются в малые, увеличенные — в уменьшенные, дважды увеличенные — в дважды уменьшенные и наоборот. Только чистые интервалы при обращении сохраняют свой вид и обращаются тоже в чистые интервалы. Сумма тонов обоих взаимообращающихся интервалов всегда равняется 6 тонам (то есть тоновой величине чистой октавы):
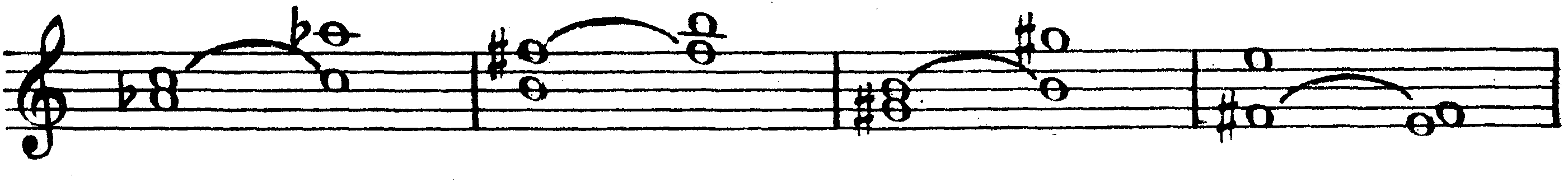
Дата добавления: 2015-04-21; просмотров: 1479;
