Резонансы в цепях синусоидального тока

Резонансом называется такой режим работы цепи, включающей в себя индуктивные и емкостные элементы, при котором ее входное сопротивление (входная проводимость) вещественно. Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением.

Резонанс в цепи с последовательно соединенными элементами
(резонанс напряжений)

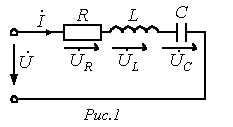Для цепи на рис.1 имеет место

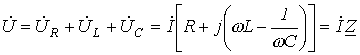
где

;

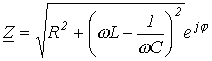(1)

.

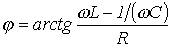(2)

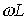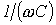В зависимости от соотношения величин и возможны три различных случая.

1. В цепи преобладает индуктивность, т.е. 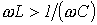, а следовательно,

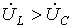. Этому режиму соответствует векторная диаграмма на рис. 2,а.

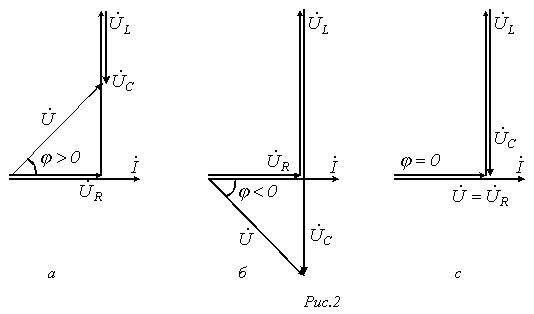
2. В цепи преобладает емкость, т.е. 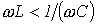, а значит, 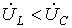. Этот случай отражает векторная диаграмма на рис. 2,б.

3. - случай резонанса напряжений (рис. 2,в).

Условие резонанса напряжений

.

(3)

При этом, как следует из (1) и (2), .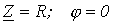

При резонансе напряжений или режимах, близких к нему, ток в цепи резко возрастает. В теоретическом случае при R=0 его величина стремится к бесконечности. Соответственно возрастанию тока увеличиваются напряжения на индуктивном и емкостном элементах, которые могут во много раз превысить величину напряжения источника питания.

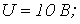
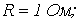
Пусть, например, в цепи на рис. 1 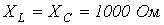. Тогда 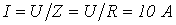, и, соответственно, .

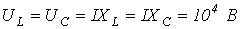Явление резонанса находит полезное применение на практике, в частности в радиотехнике. Однако, если он возникает стихийно, то может привести к аварийным режимам вследствие появления больших перенапряжений и сверхтоков.

Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной.

Суть дела не меняется, если в цепи имеется несколько индуктивных и емкостных элементов. Действительно, в этом случае 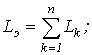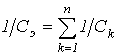, и соотношение (3) выполняется для эквивалентных значений L_Э и C_Э .

Как показывает анализ уравнения (3), режима резонанса можно добиться путем изменения параметров L и C, а также частоты. На основании (3) для резонансной частоты можно записать

.

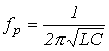(4)

Резонансными кривыми называются зависимости тока и напряжения от частоты. В качестве их примера на рис. 3 приведены типовые кривые I(f); и 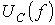для цепи на рис. 1 при U=const.

Важной характеристикой резонансного контура является добротность Q, определяемая отношением напряжения на индуктивном (емкостном) элементе к входному напряжению:

,

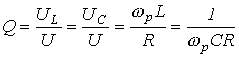(5)

- и характеризующая “избирательные” свойства резонансного контура, в частности его полосу пропускания .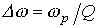

Другим параметром резонансного контура является характеристическое сопротивление, связанное с добротностью соотношением

,

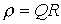(6)

или с учетом (4) и (5) для 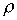можно записать:

.

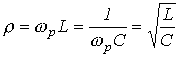(7)

Резонанс в цепи с параллельно соединенными элементами
(резонанс токов)

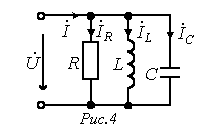Для цепи рис. 4 имеем

,

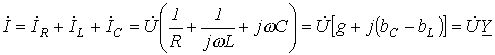где

;

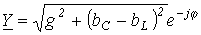(8)

.

(9)

В зависимости от соотношения величин и , как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.

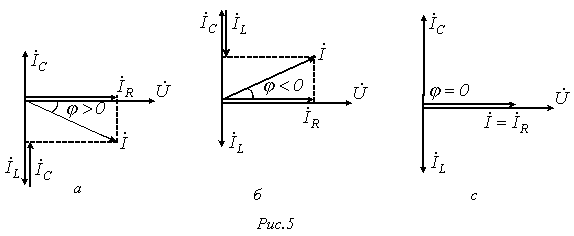
В цепи преобладает индуктивность, т.е. , а следовательно, . Этому режиму соответствует векторная диаграмма на рис. 5,а.

В цепи преобладает емкость, т.е. , а значит, 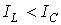. Этот случай иллюстрирует векторная диаграмма на рис. 5,б.

- случай резонанса токов (рис. 5,в).

Условие резонанса токов или

.

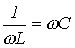(10)

При этом, как следует из (8) и (9), 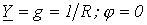. Таким образом, при резонансе токов входная проводимость цепи минимальна, а входное сопротивление, наоборот, максимально. В частности при отсутствии в цепи на рис. 4 резистора R ее входное сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе токов ток на входе цепи минимален.

Идентичность соотношений (3) и (5) указывает, что в обоих случаях резонансная частота определяется соотношением (4). Однако не следует использовать выражение (4) для любой резонансной цепи. Оно справедливо только для простейших схем с последовательным или параллельным соединением индуктивного и емкостного элементов.

При определении резонансной частоты в цепи произвольной конфигурации или, в общем случае, соотношения параметров схемы в режиме резонанса следует исходить из условия вещественности входного сопротивления (входной проводимости) цепи.

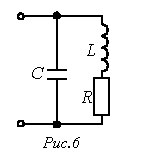Например, для цепи на рис. 6 имеем

Поскольку в режиме резонанса мнимая часть 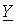должна быть равна нулю, то условие резонанса имеет вид

,

откуда, в частности, находится резонансная частота.