Гидравлический удар в трубопроводах
Гидравлическим ударом в трубах называется резкое увеличение давления при очень быстром (практически мгновенном) уменьшении скорости движения жидкости (например, при очень быстром закрытии пробкового крана). Всестороннее изучение гидравлического удара началось в связи с частыми авариями на новых линиях Московского водопровода, построенных в конце XIX века. Причины аварии исследовал выдающийся русский ученый Н.Е. Жуковский, которой впервые разработал теорию гидроудара.
Основная схема физического процесса явления гидравлического удара по теории Н.Е. Жуковского заключается в следующем (рисунок 3.36).





Рисунок 3.36 - Схема физического процесса явления гидравлического удара
Будем считать жидкость не вязкой, а сжимаемой и подчиняющейся закону Гука, а трубопровод абсолютно жестким. Физический процесс, протекающий при гидравлическом ударе, представляет собой четыре фазы преобразования энергии движущейся жидкости.
Первая фаза. При внезапном и полном закрытии задвижки в конце трубопровода вся движущаяся в нем жидкость должна остановиться. Реальная жидкость, обладающая свойством упругости, останавливается постепенно, сжимаясь от слоя к слою, начиная от конца трубопровода. Фронт остановившейся жидкости (сечение n–n) будет перемещаться от задвижки к резервуару. В остановившемся объеме между задвижкой и сечением n–n возникает дополнительное давление Dр. Скорость перемещения этого фронта называется скоростью распространения ударной волны и обозначается символом 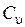
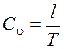 ,
,
где l и Т – соответственно длина трубы и длительность первой фазы.
Таким образом, упругая деформация сжатия и повышения давления распространяется вверх по течению и за время T достигает конца трубы. При этом освободившееся пространство на расстоянии Dl заполняется жидкостью из резервуара.
В конце первой фазы вся жидкость в трубе неподвижна ( 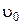 = 0) и находится под давлением р + Dр.
= 0) и находится под давлением р + Dр.
Вторая фаза. Начало второй фазы совпадает с концом первой. Жидкость в трубе сжата, но не уравновешена давлением в резервуаре, где давление p. Поэтому жидкость в трубе начинает расширяться в сторону резервуара. Сначала приобретают движение слои жидкости, близкие к резервуару, а затем фронт спада давления n–n станет перемещаться от резервуара к задвижке со скоростью 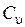 .
.
К концу второй фазы вся жидкость в трубе окажется в движении со скоростью 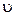 в сторону резервуара и давление в трубе восстановится до первоначального.
в сторону резервуара и давление в трубе восстановится до первоначального.
Третья фаза. (Фаза растяжения и остановки движения). В начальный момент вся жидкость движется в обратную сторону и стремится оторваться от задвижки.
Если отрыва не произойдет, то начнется растяжение жидкости с дальнейшим понижением давления до р² = р – Dр. В конце третьей фазы вся жидкость останавливается и находится под действием пониженного давления.
Это состояние оказывается также неуравновешенным, т.к. давление в резервуаре равно р, а в трубе р – Dр.
Четвертая фаза. (Фаза восстановления движения до состояния, имевшего место перед закрытием задвижки). В начале четвертой фазы жидкость из резервуара начнет втекать в трубку со скоростью 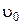 и давление будет повышаться до р. Фронт первоначального давления n–n будет перемещаться в сторону задвижки со скорость распространения ударной волны
и давление будет повышаться до р. Фронт первоначального давления n–n будет перемещаться в сторону задвижки со скорость распространения ударной волны 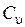 . К концу четвертой фазы скоростью движения по всей длине трубы будет равна
. К концу четвертой фазы скоростью движения по всей длине трубы будет равна 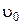 , а давление р.
, а давление р.
Так как задвижка закрыта, то, начиная с конца четвертой фазы, процесс гидравлического удара будет повторяться.
В реальных условиях, когда существуют гидравлические сопротивления и упругие деформации стенок трубопровода, процесс гидравлического удара будет более сложным и затухающим. При этом наиболее опасным является первое повышение давления (рисунок 3.37).
Время одного цикла, включающего повышение и понижение давления, называется фазой удара T. Считая скорость ударной волны при повышении и понижении давления одинаковой, определим фазу удара
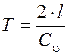 .
.


Рисунок 3.37 – Колебания давления при гидравлическом ударе
Если время закрытия задвижки меньше или равно фазе удара (t3£T), то удар называется прямым.
При t3 ³ T не вся кинетическая энергия переходит в потенциальную энергию давления и повышение давления при тех же условиях меньше, чем при прямом ударе. Такой удар называется непрямым.
Так как характеристики движения жидкости при гидравлическом ударе изменяются с течением времени, то такой процесс называется неустановившимся.
Рассмотрим гидравлический удар в трубопроводе при внезапном (мгновенном) закрытии задвижки в конце трубопровода с учетом реальных условий движения жидкости, а именно: жидкость сжимаема, а стенки трубопровода обладают упругими свойствами.


Рисунок 3.38 – Иллюстрация гидравлического удара
За бесконечно малый промежуток времени dt после закрытия задвижки движение жидкости прекращается на расстоянии 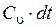 от задвижки. На этом бесконечно малом участке трубопровода произойдет повышение давления на величину Dр (рисунок 3.38).
от задвижки. На этом бесконечно малом участке трубопровода произойдет повышение давления на величину Dр (рисунок 3.38).
Определим величину Dр с помощью закона изменения количества движения. До закрытия задвижки количество движения в рассматриваемом объеме было равно
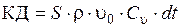 ,
,
где S – площадь сечения трубы;
r – плотность жидкости;
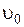 – скорость движения жидкости;
– скорость движения жидкости;
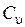 – скорость распространения ударной волны.
– скорость распространения ударной волны.
После закрытия задвижки скорость и количество движения уменьшились до нуля, т.е. в этом случае изменение количества движения стало равно начальному количеству движения. Это изменение количества движения должно быть равно импульсу действующих сил.
Учитывая, что давление в сечении 1–1 равно р0, а в сечении 2–2 повысилось до р0 + Dр, находим импульс действующих сил в виде
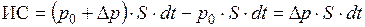
Запишем закон изменения количества движения с учетом выражений для количества движения и импульса действующих сил
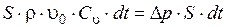 .
.
Откуда следует формула для определения повышения давления при прямом гидравлическом ударе при известной скорости распространения ударной волны 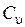 - формула Н.Е. Жуковского
- формула Н.Е. Жуковского
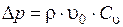 .
.
При абсолютно жестких стенках трубопровода скорость распространения ударной волны 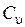 равна скорости распространения звука в воде (
равна скорости распространения звука в воде ( 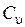 = 1425 м/с).
= 1425 м/с).
Дата добавления: 2015-04-19; просмотров: 2587;
