Гидростатическое давление и его свойства.
Рассмотрим некоторый объём жидкости, находящийся в покое (рис.1). Разделим этот объём жидкости поверхностью  на две части: левую и правую и отбросим правую часть. Для того, чтобы левая часть рассматриваемого объекта оставалась в состоянии покоя на поверхности
на две части: левую и правую и отбросим правую часть. Для того, чтобы левая часть рассматриваемого объекта оставалась в состоянии покоя на поверхности  должны быть приложены рассредоточенные силы, равнодействующую которых обозначаем через
должны быть приложены рассредоточенные силы, равнодействующую которых обозначаем через 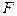 .
.
Отношение силы 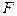 к площади
к площади  соприкосновения левой и правой частей рассматриваемого объёма жидкости будут характеризовать среднее напряжение
соприкосновения левой и правой частей рассматриваемого объёма жидкости будут характеризовать среднее напряжение  по площади
по площади 

Рис. 1. К вопросу определения гидростатического давления.
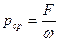
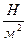 (6)
(6)
Для того, чтобы определить напряжение в некоторой точке, выделим на поверхности  элементарную площадку
элементарную площадку 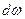 . На эту площадку будет действовать элементарная сила
. На эту площадку будет действовать элементарная сила 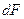 .
.
Отношение элементарной силы к элементарной площадке при стремлении последней к нулю определяет собой напряжение или гидростатическое давление в точке m:
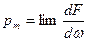 при
при  ,
, 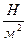 ; (7)
; (7)
| где | 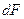
| - элементарная сила,  ; ;
|
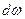
| - элементарная площадка, 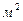 . .
|
Следовательно, гидростатическим давлением называется предел отношения элементарной силы к элементарной площадке. Или гидростатическое давление является силой, действующей в данной точке жидкости.
Другими словами, все частицы жидкости испытывают давление, как вышележащих частиц, так и внешних сил, действующих по поверхности жидкости. Действие всех этих сил и вызывает внутри жидкости напряжение, называемое гидростатическим давлением.
В международной системе единиц (СИ) за единицу давления принят 1 Паскаль (  ) – равномерно распределённое давление, при котором на 1
) – равномерно распределённое давление, при котором на 1 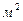 площадки приходится сила, равная 1 Н.
площадки приходится сила, равная 1 Н.
Размер единицы давления  очень мал, его значение соответствует давлению столба воды высотой
очень мал, его значение соответствует давлению столба воды высотой  . Поэтому на практике применяют единицы давления, кратные
. Поэтому на практике применяют единицы давления, кратные  , которые образуются добавлением к наименованию Паскаль приставок, общепринятых в СИ: килопаскаль (
, которые образуются добавлением к наименованию Паскаль приставок, общепринятых в СИ: килопаскаль ( 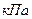 ), мегапаскаль (
), мегапаскаль ( 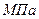 ) и гигапаскаль (
) и гигапаскаль (  ).
).
Численно указанные единицы давления составляют 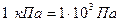 ;
;  ;
; 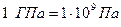 . Наиболее применяемая в технике укрупнённая единица
. Наиболее применяемая в технике укрупнённая единица 
Давление, равное 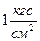 , называется технической атмосферой (ат).
, называется технической атмосферой (ат).
Пересчёт между единицами измерения гидростатического давления следующий:
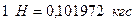 ;
; 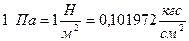 ;
; 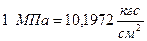 .
.
Следует заметить, что раньше в литературе по гидравлике и на практике широко использовался ряд внесистемных единиц измерения давления – физическая и техническая атмосферы, миллиметры ртутного и водяного столба.
Физическая атмосфера (атм) – давление, уравновешивающее столб ртути высотой  при плотности
при плотности  и ускорении свободного падения
и ускорении свободного падения 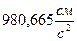 .
.
Техническая атмосфера (ат) – давление, производимое силой в 1 кгс на площадку в 1 см2.
Взаимосвязь между единицей давления, принятой в Международной системе (СИ), и применяемыми ранее единицами следующая:

Так же как сила, гидростатическое давление есть величина векторная, характеризующаяся не только величиной, но и направлением.
Гидростатическое давление обладает следующими двумя свойствами:
1. оно всегда направлено по внутренней нормали к площадке действия;
2. его величина не зависит от ориентации площадки действия, а зависит от координат рассматриваемой точки.
Первое свойство гидростатического давления следует из закона Ньютона. Так как жидкость находится в состоянии покоя, то касательные напряжения равны нулю; а напряжения, возникающие в жидкости, могут быть только нормальными. Из-за легкоподвижности жидкость в обычных условиях может находиться в состоянии покоя только под действием сжимающих усилий; поэтому гидростатическое давление может быть направлено лишь по внутренней нормали к площадке действия.
Второе свойство гидростатического давления докажем, рассматривая равновесие элементарной трёхгранной призмы, мысленно вырезанной в покоящейся жидкости (рис.2).
Проведём оси координат так, как показано на рисунке 2. Пусть ребро АВ, равное  , параллельно оси
, параллельно оси  , ребро АЕ, равное
, ребро АЕ, равное 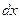 , параллельно оси
, параллельно оси  , а ребро AD параллельно оси
, а ребро AD параллельно оси  .
.
Гидростатическое давление в пределах грани АВСD примем равным 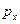 ; в пределах грани ADFE – равным
; в пределах грани ADFE – равным 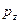 ; в пределах грани BCFE – равным
; в пределах грани BCFE – равным 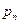 .
.

Рис 2. К вопросу второго свойства гидростатического давления.
Согласно первому свойству гидростатического давления, векторы давлений 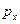 ,
, 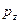 ,
, 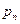 направлены нормально к соответствующим граням.
направлены нормально к соответствующим граням.
Спроецируем все силы, действующие на элементарную трёхгранную призму, на оси координат.
Проецируя все силы на ось  , получим
, получим
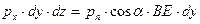 (8)
(8)
Из рис. 2 видно, что 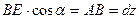 , поэтому
, поэтому 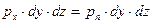 или
или
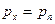 (9)
(9)
Спроецируем теперь все силы, действующие на элементарную трёхгранную призму, на ось 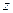 :
:
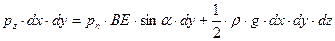 (10)
(10)
где 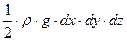 - сила тяжести объема трехгранной призмы (0,5 объема прямоугольного параллелепипеда), Н.
- сила тяжести объема трехгранной призмы (0,5 объема прямоугольного параллелепипеда), Н.
Замечая, что  и сокращая на
и сокращая на 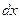 и
и 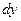 , получим
, получим
 (11)
(11)
Величина  в пределе стремится к нулю, поэтому
в пределе стремится к нулю, поэтому
 (12)
(12)
Так как наклон грани BCFE выбран произвольно, то отсюда следует, что величина гидростатического давления зависит не от ориентации площадки действия, а от координат рассматриваемой точки.
Дата добавления: 2015-04-19; просмотров: 1427;
