Обработка результатов прямых равноточных многократных измерений.

Рассмотрим группу из n независимых результатов наблюдений случайной величины x, подчиняющейся нормальному распределению.

Поскольку число наблюдений в группе, на основании которых вычислено среднее арифметическое т_x , ограничено, то, повторив заново серию наблюдений этой же величины, мы получили бы новое значение среднего арифметического. Повторив многократно серии наблюдений и, вычисляя каждый раз их среднее арифметическое значение, принимаемое за результат измерения, мы убедимся в рассеянии средних арифметических значений. Характеристикой этого рассеяния является среднее квадратическое отклонение среднего арифметического .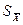

.

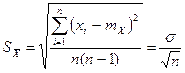Среднее квадратическое отклонение 5₇ используется для оценки погрешности результата измерений с многократными наблюдениями.

Теория показывает, что если рассеяние результатов наблюдений в группе подчиняется нормальному закону, то и их среднее арифметическое тоже подчиняется нормальному закону распределения при достаточно большом числе наблюдений (n > 50). Отсюда следует, что при одинаковой доверительной вероятности, доверительный интервал сред-

него арифметического в √n раз уже доверительного интервала результата наблюдений. Теоретически, при n → ∞ случайную погрешность результата измерения можно было бы свести к нулю. Однако это невозможно, и стремиться беспредельно уменьшать случайную погрешность результата измерения не имеет смысла, так как рано или поздно определяющим становится не рассеяние среднего арифметического, а недостоверность поправок на систематическую погрешность (неисключенная систематическая погрешность).

При нормальном законе распределения плотности вероятностей результатов наблюдений и небольшом числе наблюдений среднее арифметическое подчиняется закону распределения Стьюдента с тем же средним арифметическим значением т_x. Особенностью этого распределения является то, что доверительный интервал с уменьшением числа наблюдений расширяется, по сравнению с нормальным законом распределения при той же доверительной вероятности. Для оценки доверительных границ случайной погрешности это отражается введением коэффициента t_qвместо t. Коэффициент t_qраспределения Стьюдента зависит от числа наблюдений и выбранной доверительной вероятности м находится по таблице. Так, при числе наблюдений n = 14 и доверительной вероятности Р = 0,95 t_q = 2,16.

Правила обработки результатов измерения с многократными наблюдениями учитывают следующие факторы:

- обрабатывается ограниченная группа из nнаблюдений;

- результаты наблюдений x_iмогут содержать систематическую погрешность;

- в группе наблюдений могут встречаться грубые погрешности;

- распределение случайных погрешностей может отличаться от нормального.

Обработка результатов наблюдений производится в следующей последовательности:

1. Исключить известные систематические погрешности из результатов наблюдений (введением поправки).

2. Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения:

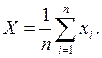
3. Вычислить оценку среднего квадратического отклонения результатов наблюдения

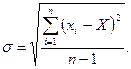
Вычислив оценку СКО результата наблюдений, целесообразно проверить наличие в группе наблюдений грубых погрешностей, помня, что при нормальном законе распределения ни одна случайная погрешность x_i – X,с вероятностно практически равной единице, не может выйти за пределы ±3σ. Наблюдения, содержащие грубые погрешности, исключают из группы и заново повторяют вычисления Xи σ.

4. Вычислить оценку СКО результата измерения .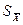

5. Проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению.

Приближенно о характере распределения можно судить, построив гистограмму. Строгие методы проверки гипотез с использованием специальных критериев (χ² — Пирсона, ω² — Мизеса-Смирнова и др.) рассматриваются в специальных дисциплинах.

При числе наблюдений n < 15 принадлежность их к нормальному распределению не проверяют, а доверительные границы случайной погрешности результата определяют лишь в том случае, если достоверно известно, что результаты наблюдений принадлежат нормальному закону.

6. Вычислить доверительные границы е случайной погрешности ре-зультата измерения при заданной вероятности Р:

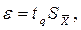
где t_q — коэффициент Стьюдента.

7. Вычислить границы суммарной неисключенной систематической погрешности (НСП) результата измерений.

Неисключенная систематическая погрешность результата образуется из неисключенных систематических погрешностей метода, средств измерений, погрешностей поправок и др.

При суммировании эти составляющие рассматриваются как случайные величины. При отсутствии данных о виде распределения неисключенных составляющих систематических погрешностей их распределения принимают за равномерные. При равномерном распределении неисключенных систематических погрешностей границы неисключенной систематической погрешности результата измерения 0 вычисляют по формуле

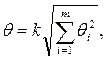
где θ_i — граница i-й неисключенной составляющей систематической погрешности; k — коэффициент, определяемый принятой доверительной вероятностью (при Р = 0,95

k = 1,1); т — количество неисключенных составляющих.

Доверительную вероятность для вычисления границ НСП принимают той же, что при вычислении границ случайной погрешности результата измерения.

8. Вычислить доверительные границы погрешности результата измерения.

Анализ соотношения между неисключенной систематической погрешностью и случайной погрешностью показывает, что если 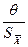< 0,8, то неисключенной систематической погрешностью можно пренебречь и принять границы погрешности результата Δ равным ±ε . Если 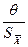> 8, то случайной погрешностью можно пренебречь и принять границы погрешности результата Δ равным ±θ .

Если оба неравенства не выполняются, вычисляют СКО результата как сумму неисключенной систематической погрешности и случайной составляющей:

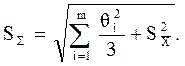
Границы погрешности результата измерения в этом случае вычисляют по формуле

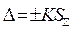
Коэффициент К вычисляют по эмпирической формуле

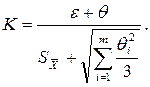
Стандартом регламентирована и форма записи результатов измерений. При симметричном доверительном интервале погрешности результат измерения представляют в форме X ± Δ, Р, где X— результат измерения,

При отсутствии данных о видах функции распределения составляющих погрешности результата или при необходимости дальнейшей обработки результатов, результат измерения представляют в форме X, S_x, n, θ.