Теория оптического нитяного дальномера и его устройство

В сетке нитей зрительных труб, как правило, имеются две дополнительные горизонтальные нити, расположенные по обе стороны от центра сетки нитей на равных расстояниях от него; это - дальномерные нити (рис.4.25).

Нарисуем ход лучей, проходящих через дальномерные нити в трубе Кеплера с внешней фокусировкой. Прибор установлен над точкой А; в точке В находится рейка, установленная перпендикулярно визирной линии трубы. Требуется найти расстояние между точками А и В.

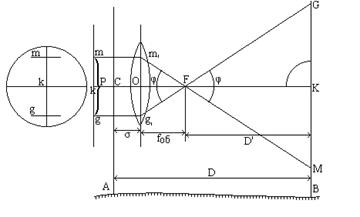
Рис.4.25

Построим ход лучей из точек m и g дальномерных нитей. Лучи из точек m и g, идущие параллельно оптической оси, после преломления на линзе объектива пересекут эту ось в точке переднего фокуса F и попадут в точки М и G рейки. Расстояние от точки A до точки B будет равно:

D = l/2 * Ctg(φ/2) + fоб + d, (4.33)

где d - расстояние от центра объектива до оси вращения теодолита;
f_об-фокусное расстояние объектива;
l - длина отрезка MG на рейке.

Обозначим (f_об + d) через c, а величину 1/2*Ctg φ/2 - через С, тогда

D = C * l + c. (4.34)

Постоянная С называется коэффицентом дальномера. Из Dm'OF имеем:

Ctg φ/2 = ОF/m'O; m'O= p/2; Ctg φ/2 = (fоб*2)/p,

где p - расстояние между дальномерными нитями. Далее пишем:

С = f_об/p. (4.35)

Коэффициент дальномера равен отношению фокусного расстояния объектива к расстоянию между дальномерными нитями. Обычно коэффицент С принимают равным 100, тогда Ctg φ/2 = 200 и φ = 34.38'. При С = 100 и fоб = 200 мм расстояние между нитями равно 2 мм.