Вероятнейшее значение измеряемой величины

Пусть имеется ряд равноточных измерений величины X:

l₁, l₂ , ..., l_n .

Вычислим арифметическую середину X₀ = [1]/n и образуем разности:

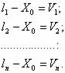(1.38)

Сложим все разности и получим [l] - n ∙ X₀ = [V]. По определению арифметической середины n ∙ X₀ = [l], поэтому:

[V] = 0. (1.39)

Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:

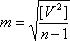(1.40)

Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:

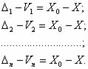(1.41)

Разность (X₀ - X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):

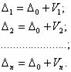(1.42)

Возведем все уравнения (1.42) в квадрат, сложим их и получим:

.

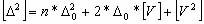Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,

.

Разделим это уравнение на n и учтя, что [Δ²]/n =m², получим:

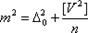(1.43)

Заменим истинную ошибку арифметической середины Δ₀ ее средней квадратической ошибкой 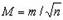; такая замена практически не изменит правой части формулы (1.43). Итак,

,
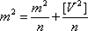откуда ;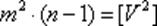

после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).