Измерения, и их классификация

Измерения являются важной составной частью геодезических работ; именно из измерений получают количественную информацию о различных объектах, подлежащих изучению. Геодезистам приходится измерять длины линий, горизонтальные и вертикальные углы, превышения между точками местности, температуру воздуха, ускорение свободного падения, интервалы времени и многое другое. Результаты измерений могут использоваться как непосредственно, так и как промежуточные величины для вычисления таких характеристик объекта, которые либо вообще нельзя измерить, либо их измерение требует слишком больших затрат времени и средств.

Методика выполнения измерений разрабатывается конкретно для каждого вида измерений и имеет целью достичь необходимую точность результатов при наименьшей трудоемкости процесса.

С точки зрения теории обработки измерений все измерения нужно разделить на необходимые и избыточные. Если количество неизвестных величин равно t, а количество измерений равно n, причем n>t, то t измерений являются необходимыми, а (n-t) - избыточными.

Простой пример: чтобы узнать значение угла, достаточно измерить его один раз (t=1); на практике угол измеряют несколькими приемами, получая n его значений; следовательно, (n-1) измерений избыточны.

Все измерения сопровождаются ошибками, и главная задача обработки измерений - устранение противоречий между результатами измерений, содержащими ошибки, и математической моделью, включающей численные значения измеряемых величин. Решение этой задачи из-за наличия избыточных измерений неоднозначно, поэтому для получения единственного решения на него накладывают одно или несколько дополнительных условий. В геодезии такое условие записывают в виде:

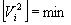, (1.23)
или
, (1.24)

то-есть, из всех возможных решений выбирается такое, в котором сумма квадратов поправок Vi в результаты измерений имеет наименьшее значение; буквой pi обозначен вес i-того измерения.

В теории обработки измерений для знака «сумма» используются два символа: ∑ и [ ].

Обработку измерений при наличии избыточных измерений под условием (1.23) или (1.24) называют уравниванием по методу наименьших квадратов, сокращенно МНК. В зарубежной литературе вместо термина «уравнивание по МНК» часто используют термин «оценивание по МНК».

Уравнивание по МНК можно выполнять двумя способами; первый называется параметрическим, второй - коррелатным. Обозначим через n общее количество измерений, через t - количество определяемых элементов и через r - количество избыточных измерений (r = n - t).

В первом способе сначала получают приближенные значения определяемых элементов, сводя задачу к нахождению t параметров-поправок к этим приближенным значениям. Затем составляют n параметрических уравнений (по количеству измерений), преобразуют их и получают t нормальных уравнений с t неизвестными параметрами. Решают нормальные уравнения, затем вычисляют значения определяемых элементов и выполняют оценку точности.

Во втором способе составляют r условных уравнений с n неизвестными поправками к результатам измерений и после их преобразования получают r нормальных уравнений с r неизвестными вспомогательными множителями, лназываемыми коррелатами. Решают все r уравнений как систему, находят значения коррелат и по ним вычисляют поправки к измерениям; определяемые элементы вычисляют по значениям исправленных измерений любым из возможных способов.

Трудоемкость того или другого варианта при ручном счете зависит от соотношения t и r; если t > r, то предпочтительнее второй вариант, если t < r, то - первый. При счете на ЭВМ как правило используют первый вариант.

В результате уравнивания достигают следующих целей:

вычисляют наиболее надежные, наиболее достоверные значения неизвестных величин,

вычисляют и оценивают поправки в измеренные элементы для при ведения их в соответствие с геометрическими условиями конкретной модели,

выполняют оценку точности уравненных элементов модели.