Применение геометрических (лучевых) отражений и их построение

В зале звуковые волны распространяются от источника к ограждающим поверхностям, от которых многократно отражаются. В результате в помещении образуется звуковое поле.

Приближенная оценка формы и размеров помещений с акустической точки зрения состоит в анализе звукового поля на основе принципов геометрической акустики, то есть в рассмотрении распространения прямых и отраженных звуковых волн и построении так называемого "лучевого эскиза".

При определенных условиях можно вместо звуковых волн рассматривать звуковые лучи, в направлении которых распространяются эти волны. Распространение таких лучей аналогично распространению световых лучей в геометрической оптике, и построение геометрических (лучевых) отражений широко применяется в архитектурной акустике:

1) падающий и отраженный от какой-либо точки поверхности лучи образуют равные углы (угол падения и угол отражения) с нормалью к отраженной поверхности в этой точке;

2) падающий и отраженный лучи лежат совместно с нормалью в одной плоскости (лучевая плоскость).

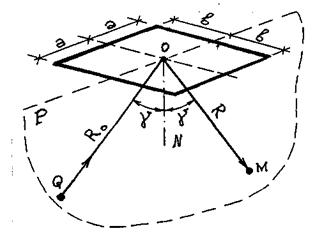
Рис. 10. Отражение звука от прямоугольного отражателя

Допустимость применения геометрических (лучевых) отражений зависит от длины звуковой волны, размеров отражающей поверхности и ее расположения по отношению к источнику звука и точке приема. Отражающая поверхность должна при этом иметь массу не менее 20 кг/м² , и ее коэффициент звукопоглощения α для рассматриваемых частот не должен превышать 0,1. На рис. 10 отражающая поверхность взята в виде прямоугольного плоского отражателя со сторонами, равными 2a и 2b, центр его совпадает с точкой геометрического отражения О, а сторона 2 а параллельна лучевой плоскости P , в которой лежат падающий луч QO , отраженный луч ОМ и нормаль ОN; R₀ - расстояние от источника Q до точки O; R - расстояние от точки O до точки приема М; g - углы падения и отражения. Если ввести безразмерные величины

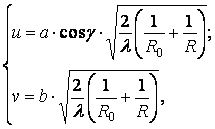(6)

где l - длина звуковой волны, то абсолютное отклонение фактического уровня звукового давления в точке приема М от уровня, соответствующего строго геометрическому отражению, не превысит, дБ:

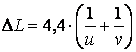(7)

Применение геометрических отражений можно считать допустимым если DL не более 5 дБ, а наименьшая сторона отражателя не менее чем в 1,5 раза превышает дайну волны l. Длина волны l связана с частотой f.

Если форма и ориентировка отражателя отличаются от показанных на рис. 10, то расчет значительно усложняется. Для ориентировочной оценки отклонения от геометрической акустики можно приближенно использовать формулу (7), вписав в отражатель прямоугольник, удовлетворяющий рис. 10.

Формула (7) применима и для отражателя, обладающего кривизной, если его наименьший радиус кривизны не менее чем в 2 раза превышает длину волны l.

Поверхности, дающие направленные отражения, следует проектировать таким образом, чтобы условия применимости геометрических отражений выполнялись, по крайней мере, для частот, превышающих 300-400 Гц (то есть для звуковых волн длиной примерно 1 м и менее), так как эти частоты важны для разборчивости речи. Таким образом, для расчета можно принимать l = 1 м. Если указанные условия выполнены, то построение геометрических отражений допустимо не только от центра отражателя но и от других точек его поверхности, удаленных от краев отражателя не менее чем в половину длины волны l. При заданном требовании l £1 м это означает, что точки геометрического отражения должны браться не ближе 0,5 м от краев отражающей поверхности.

При построении геометрических отражений от плоскости удобен прием, показанный на рис. 11 а. Здесь используется мнимый источник Q₁, симметричный с действительным точечным источником Q по отношению к отражающей плоскости и находящийся по другую ее сторону. Для построения мнимого источника надо опустить из точки Q перпендикуляр QA на отражающую плоскость и на продолжении его отложить отрезок AQ₁, равный отрезку QA . Прямые, проведенные из мнимого источника Q₁, после пересечения ими отражающей плоскости удовлетворяют условию равенства углов падения и отражения, то есть являются искомыми отраженными лучами, создаваемыми действительным источником Q.

Метод мнимых источников применим и при построении отражений от кривых поверхностей. Если требуется найти отражение от какой-либо точки O кривой поверхности С (см. рис. 11 б) при заданном положении источника Q, то следует в точке O построить касательную плоскость Т к поверхности. Мнимым источником в этом случае является точка Q₁, симметричная источнику Q относительно касательной плоскости; продолжение ОМ прямой Q₁O после пересечения ее с поверхностью С является искомым отраженным лучом. Здесь для каждой точки O отражающей поверхности приходится находить свой мнимый источник Q₁ в отличие от ранее рассмотренного случая (см. рис. II,а), у которой для отражения от любой ее точки мнимый источник один и тот же (при заданном положении источника Q). Суммарная длина QO + ОМ лучей QO и ОМ, дающая длину полного хода отраженного звука от источника Q до некотрой точки приема М, равна расстоянию Q₁M от мнимого источника Q₁ до точки М (см. рис. 11а, 11б). При этом, разумеется, следует брать истинные длины указанных отрезков, а не их проекций.

Если лучевая плоскость Р (см. рис.10) параллельна одной из плоскостей проекций (вертикальной или горизонтальной, то углы падения и отражения проецируются на эту плоскость без искажения, и построение отраженного луча выполняется при помощи описанных приемов.

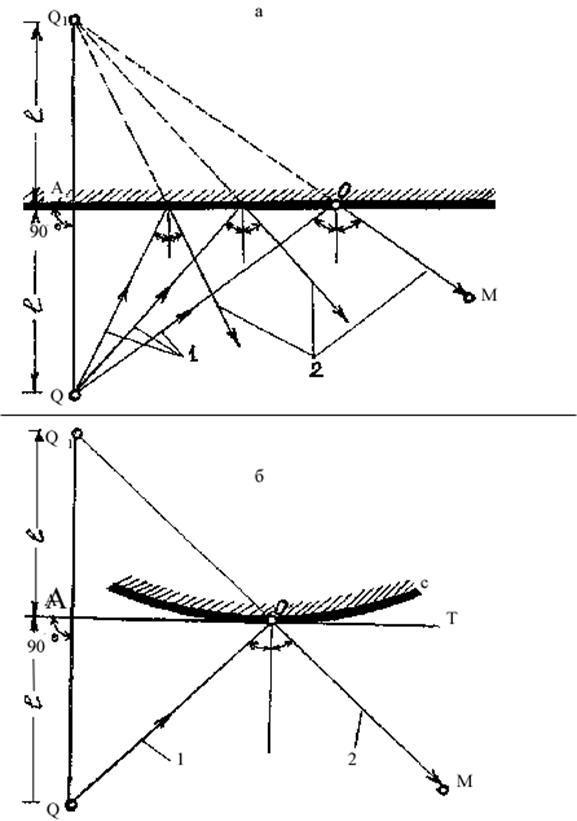
Рис. 11. Построение геометрических отражений звуковых лучей с помощью мнимого источника: а - отражение от плоскости;

б - отражение от кривой поверхности;

Q - источник звука;

Q₁ - мнимый источник звука;

1 - прямые лучи, 2 - отраженные.

Не представляет трудности построение отраженного луча и в тех случаях, когда лучевая плоскость не параллельна плоскости проекций, но ей параллельна лишь нормаль к отражающей поверхности в точке отражения. Это равносильно тому, что касательная плоскость к отражающей поверхности (в той же точке) перпендикулярна плоскости проекции.

Для примера на рис. 12 дано построение геометрического отражения, вызываемого отражателем, имеющим вид цилиндрической поверхности с произвольной криволинейной направляющей и с образующими, перпендикулярными вертикальной плоскости проекций. Отражатель помещен вблизи потолка перед эстрадой зала. Точечный источник звука задан его проекциями q и q'. Требуется найти геометрическое отражение от некоторой точки отражателя, имеющей проекции а и a'. В данном случае касательная плоскость к поверхности отражателя в этой точке перпендикулярна вертикальной плоскости проекции; вертикальная проекция этой касательной плоскости есть прямая t't'. Прямые q'a' и qa являются вертикальной и горизонтальной проекциями луча, исходящего из источника и достигающего точки отражения.

Вертикальную проекцию мнимого источника q₁' находим, опустив из точки q' перпендикуляр q'О' на прямую t't'и отложив на его продолжении отрезок О'q₁' , равный отрезку q'О'. Снося точку q₁' на горизонтальную прямую, проходящую через точку q, находим горизонтальную проекцию мнимого источника q₁. Продолжения прямых q₁'a' и q₁а, лежащие вправо от точек a'и a, являются соответственно вертикальной и горизонтальной проекциями отраженного луча.

Вертикальная проекция отраженного луча пересекает в точке e' расчетную поверхность амфитеатра (проходящую на 1,2 м выше его пола, соответственно положению ушей слушателей). Снося точку е' на горизонтальную проекцию отраженного луча, находим горизонтальную проекцию е точки пересечения отраженного луча с расчетной поверхностью амфитеатра. Длина ломаной линии, имеющей проекции qae и q'a'e', равна полному ходу отраженного звука от источника до точки приема с проекциями e и e' . Эта длина равна расстоянию от мнимого источника до точки приема. Прямая с проекциями qe и q'е' дает ход прямого звука. На рис. 12 легко найти и ходы прямого и отраженного звука. Так, например, полный ход отраженного звука (от источника до точки приема) равен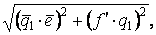

где f - точка пересечения горизонтальной прямой, проведенной через точку e', с вертикальной прямой q'₁q₁.

В случаях, когда касательная плоскость к отражающей поверхности не перпендикулярна ни к одной из плоскостей проекций, надо при помощи обычных методов начертательной геометрии (замена плоскостей проекций, вращение) перейти к конфигурации, в которой касательная плоскость станет перпендикулярной плоскости проекций.

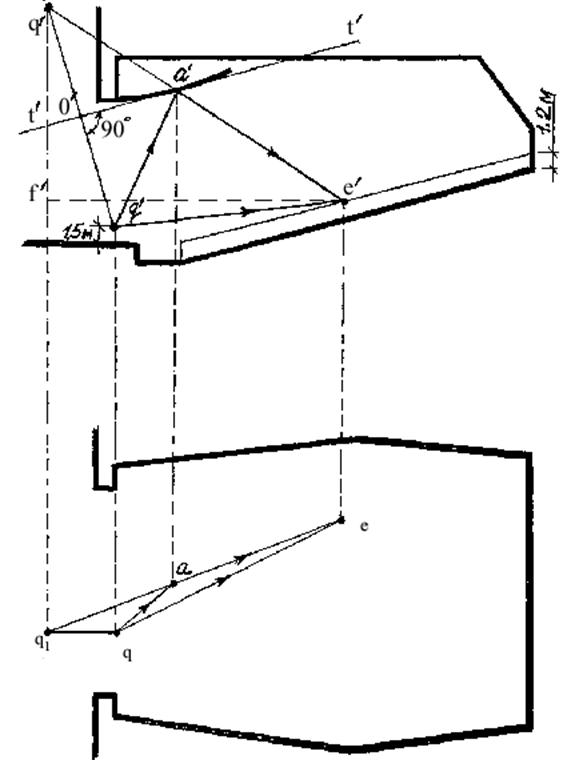
Рис. 12. Построение геометрического отражения при касательной плоскости, перпендикулярной плоскости проекции