Термодинамические процессы изменения состояния водяного пара

Изохорный процесс. В изохорном процессе при подводе теплоты к влажному пару увеличиваются его давление и температура. При v — const степень сухости с уменьшением темпера-_v туры может как убывать, так и возрастать. Если начальное состояние вещества находится вблизи кривой х — О, то с уменьшением температуры при v — const степень сухости увеличивается. Если начальное состояние вещества находится вблизи кривой к = 1, то с уменьшением температуры при v = const степень сухости уменьшается.

В изохорном процессе внешняя работа равна нулю. Подведенная теплота расходуется на изменение внутренней энергии рабочего тела:

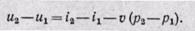
Если удельный объем и процесса меньше объема сухого насыщенного пара v" конечного состояния о<Х, то в конце процесса пар будет влажным; если о>v", то пар будет перегретым.

Степень сухости влажного пара можно определить по формуле

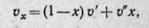откуда

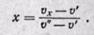(12-6)

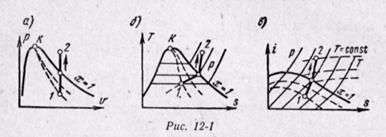
На рv-диаграмме изохорный процесс изображается отрезком прямой, параллельной оси ординат (рис. 12-1, а), на Ts-диаграмме, процесс изображается кривой линией (рис. 12-1, б). В области влажного пара изохора направлена выпуклостью вверх, а в области перегретого пара — вниз. На is-диаграмме изохора изображается кривой, направленной выпуклостью вниз (рис. 12-1, в).

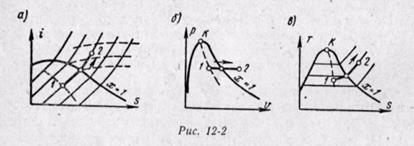
Изобарный процесс. На is-диаграмме изобара в области насыщенного пара представляется прямой линией, пересекающей нижнюю, и верхнюю пограничные кривые. При подводе теплоты к влажному пару степень сухости его увеличивается и он (при постоянной температуре) переходит в сухой, а при дальнейшем подводе теплоты в перегретый пар. Изобара в области перегретого пара представляет собой кривую, направленную выпуклостью вниз (рис. 12-2, а).

На рv-диаграмме изобарный процесс изображается отрезком горизонтальной прямой, который в области влажного пара представляет собой и изотермический процесс одновременно (рис. 12-2, б). На Ts-диаграмме в области влажного пара изобара изображается прямой линией, а в области перегретого пара — кривой, обращенной выпуклостью вниз (рис. 12-2, в). Значения всех необходимых величин для расчета берутся из таблиц насыщенных и перегретых паров.

Изменение внутренней энергии пара

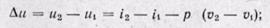
внешняя работа

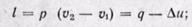
количество подведенной теплоты

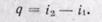
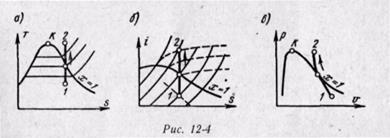
В том случае, когда величина q задана и требуется найти параметры второй точки, лежащей в области двухфазных состояний, применяется формула для энтальпии влажного пара

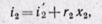(12-7)

откуда находится степень сухости x₂, зная которую можно легко найти остальные параметры.

Изотермический процесс. На is-диаграмме в области влажного пара изотерма совпадает с изобарой и является прямой наклонной линией. В области перегретого пара изотерма изображаетёя кривой с выпуклостью вверх (рис. 12-3, а).

На рv-диаграмме в области влажного пара изотермический процесс изображается горизонтальной прямой. Для насыщенного пара

\

этот процесс совпадает с изобарным. В области перегрева давление пара понижается, а процесс изображается кривой с выпуклостью к осп абсцисс (рис. 12-3, б). На Ts-диаграмме изотермический процесс изображается отрезком горизонтали (рис. 12-3, в).

Внутренняя энергия водяного пара в отличие от внутренней энергии идеального газа изменяется вследствие изменения потенциальной составляющей и поэтому

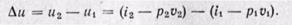
Количество подведенной теплоты в процессе равно

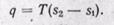
Внешняя работа определяется как

l = q — Δu.

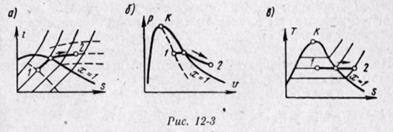
Адиабатный процесс. Адиабатный процесс совершается без подвода и отвода теплоты, и энтропия рабочего тела при обратимом процессе остается постоянной величиной - s = const. Поэтому на is- и Ts-диаграммах адиабаты изображаются вертикальными прямыми (рис. 12-4, а, 12-4, б). При адиабатном расширении давление и температура пара уменьшаются; перегретый пар переходит в сухой, а затем во влажный. Из условий постоянства энтропии возможно определение конечных параметров пара, если известны параметры начального и один параметр конечного состояний.

На рv-диаграмме обратимый адиабатный процесс изображается некоторой кривой (рис. 12-4, в).

Работа в адиабатном процессе определяется из уравнения

l = u₁ — u₂ = (i₁ — p₁v₁) — (i₂ — p₂v₂). Изменение внутренней энергии будет

Δu = (i₂ — p₂v₂) — (i₁ — p₁v₁).