Основные теоретические сведения
Четырехполюсником называется часть электрической цепи, имеющая два входных и выходных зажима.
Изображается четырехполюсник в виде прямоугольника с выходящими из него зажимами 1-1' и 2-2' (рис.8-1).

Рис.8-1
Если внутри четырехполюсника отсутствуют источники энергии, четырехполюсник называется пассивным. Зажимы четырехполюсника 1-1' будем считать входными, 2-2' выходными.
Уравнения, связывающие входные и выходные токи и напряжения, могут быть записаны в различных формах:
А , Y , Z , H , G , B.
При записи уравнений в форме А пассивный четырехполюсник характеризуется четырьмя коэффициентами А, В, С, D, которые входят в линейные уравнения, связывающие напряжения и токи на входе и навыходе четырехполюсника при любой нагрузке на выходных зажимах.
U1 = A U2 + B I2 (8.1)
I1 = C U2 + D I2(8.2)
Указанные коэффициенты, называемые постоянными четырахполюсника, связаны между собой равенством
АD - ВС = 1(8.3)
Из уравнения (8.3) следует, что из четырех коэффициентов независимыми являются только три.
Если у четырехполюсника поменять местами входные и выходные зажимы (рис.8-2)

Рис.8-2.
то получим уравнения:
U1 = A'U2 + B'I2 ,
I1 = C'U2 + D'I2 ,
где А'=D, В'=В, С'=С , D'=А.
Уравнения четырехполюсника при "обратном", питании записываются в виде
U1 = D U2 + B I2 , I1 = C U2 + A I2.
Четырехполюсник называется симметричным, если при перемене местами источника питания инагрузки,токи в источнике питания и нагрузке не изменяются. В симметричном четырехполюснике А = D.
Комплексные коэффициенты А, В, С, D, входящие в уравнения (8.1) , (8.2) , можно определить аналитически по известной схеме соединений внутри четырехполюсника, а также экспериментально, когда внутреннее строение четырехполюсника неизвестно.
Комплексные входные сопротивления находят опытными путем с помощью ваттметра, амперметра и вольтметра. Производится обычно четыре опыта: опыт холостого хода и опыт короткого замыкая при "прямом питании" и то же при "обратном".
Для расчета необходимо лишь три опыта. Четвертый опыт служит для проверки.
Для каждого из этих опытов уравнения четырехполюсника запишутся:
Прямое питание:
U1X = A U2X , - опыт холостого хода ( I2 = 0 ).
I1X = C U2X .
U1K = B U2K , - опыт короткого замыкания ( U2=0 ).
I1K = C U2K
Обратное питание:
U1X = D U2X , - опыт холостого хода ( I2 = 0 ).
I1X = C U2X
U1K = B I1K , - опыт короткого замыкания ( U2=0 ).
I1K = A I1K
Из этих выражений получаем комплексные входные сопротивления четырехполюсника:
при прямом питании:
Z1X = U1X/ I1X = A / C, Z1K = U1K/ I1K = B / D.
при обратном питании:
Z2X = U1X/ I1X = D / C, Z2K = U1K/ I1K = B / A.
Комплексные входные сопротивления в каждом из опытов, определяются по показаниям амперметра, вольтметра и ваттметра.
Zbx = zbx e jφ,
где zbx = Ubx / Ibx ; φ = arctg(P / (Ubx·Ibx)).
Используя результаты опытов холостого хода и короткого замыкания можно определить постоянные четырехполюсника
A = Z1X / √Z2X(Z1X-Z1K) , С = А / Z1X , В = А Z2K , D = B / Z1K .
Аналогичным образом можно определить постоянные четырехполюсника и других форм записи четырехполюсника.
Любой четырехполюсник может быть заменен эквивалентной схемой , состоящей из трех элементов. Таких схем замещения существует дне: Т-образная (рис. 8-3) и П-образная (рис.8-4).
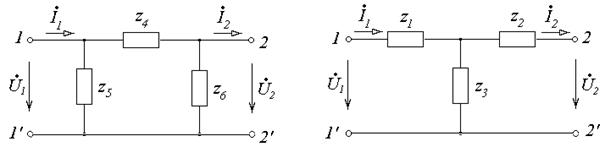
Рис.8-3 Рис.8-4
Связь между постоянными А, В, С, D четырехполюсника и эквивалентной схемой характеризуется следующими выражениями: Для Т-образной схемы:
C =1 / Z3 ; A = 1+Z1/Z3 ; B = Z1+ Z2+ ( Z1 Z2)/ Z3 ; D = 1+Z2/Z3 .
Если известны А, В, С, D, то можно определить Z1, Z2 и Z3:
Z1 = (A-1)/C ; Z2 = (D-1)/C; Z3 = 1/C .
Для П-образной схемы:
A = 1+Z4/Z6 ; В = Z4 ; С = (Z4 + Z5 + Z6)/ Z5 Z6 ; D = 1+Z4/Z5 .
и обратно
Z4 = В; Z5 = В /(D - 1) ; Z6 = B /(A - 1).
Дата добавления: 2015-04-15; просмотров: 735;
