Основные теоретические сведения. Для соединения трех однофазных приемников ZAB, ZBC, ZCA треугольником (рис.7-1) , необходимо конец Х первого приемника соединить с началом В второго

Для соединения трех однофазных приемников Z_AB, Z_BC, Z_CA треугольником (рис.7-1) , необходимо конец Х первого приемника соединить с началом В второго, конец Yвторого - с началом С третьего, конец Z третьего сначалом А первого приемника, а к узлам полученного треугольника подвести линейными проводами энергию от трехфазной сети.

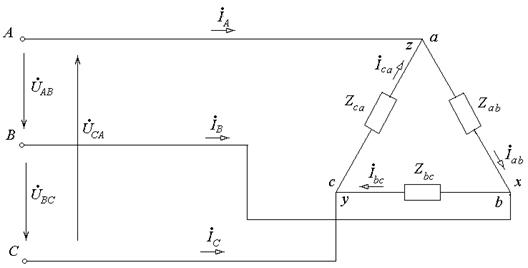
Рис.7-1. Схема соединения приемников треугольником

и включение их в трехфазную сеть.

Если комплексные сопротивления фаз нагрузки одинаковы

Z_AB = Z_BC = Z_CA = ze^jφ , (7.1)

то такую нагрузку называют симметричной.

При соединении треугольником каждый приемник включен между подводящими проводами и находится под линейным напряжением, которое одновременно является фазным напряжением U_Ф. Поэтому при соединении приемников треугольником справедливо равенство

U_Ф = U_Л. (7.2)

Ток каждого приемника, входящего в соединение треугольником, является фазным и определяется по формуле

I_Ф = U_Ф/Z_Ф , (7.3)

где U_Ф -фазное напряжение на зажимах данного приемника, Z_Ф - его полное сопротивление.

При симметричной нагрузке фазные токи всех фаз одиноковы по величине

I_AB = I_BC = I_CA = I_Ф(7.4)

и сдвинуты по отношению к своим фазным напряжениям на одинаковые углы

j_АВ = j_ВС = j_СА = j, (7.5)

определяемые формулой

j = arctg(x_ф/r_ф) ,(7.6)

где x_ф- реактивное сопротивление фазы нагрузки, r_ф- ее активное сопротивление.

В общем случае линейные токи I_{A ,} I_{B ,} I_Cи фазные токи I_AB , I_BC , I_CA связаны на основании первом закона Кирхгофа векторными уравнениями

I_A= I_AB - I_CA;

I_B= I_BC - I_AB; (7.7)

I_C= I_CA - I_BC .

Из этих уравнений вытекает, что независимо от характера нагрузки всегда справедливо равенство

I_A + I_B + I_C =0 (7.8)

При симметричной нагрузке фаз все линейные токи равны между собой и превышают значения фазных токов в раз, т.е.

I_Л= I_Ф=1,73 I_Ф (7.9)

Векторы линейных напряжений могут изображаться либо симметричной звездой , либо равносторонним треугольником. Эти напряжения практически неизменны.

При симметричной нагрузке фаз векторы линейных токов сдвинуты относительно векторов фазных токов на 30° (pиc.7-2).

Фазные токи сдвинуты относительно фазных напряжений на одинаковые углы j , а линейные токи определяются как геометрические разности соответствующих фазных токов (рис.7-2а).

При несимметричной нагрузке фаз, имеющей место при несоблюдении равенства (7.1) , нарушается симметрия как фазных, так и линейных токов, что видно из векторной диаграммы напряжений токов (рис.7-2б).

а) б)

Рис.7-2. Векторная диаграмма напряжений и токов при: а) при симметричной нагрузке, б) несимметричной нагрузке

Обрыв одного из линейных проводов нарушает нормальный режимработы установки, при этом приемники только одной фазы будут находиться под номинальным фазным напряжением, а приемники двух других фаз окажутся последовательно соединенными и будут питаться от этого же напряжения, которое обусловит установление на их зажимах напряжений, прямо пропорциональных величинам полных их сопротивлений. Следовательно, эти приемники окажутся под напряжением , отличающимся от номинального значения фазного напряжения. В случае преобладания в одной из фазиндуктивной, а в другой - емкостной нагрузки может возникнуть резонанс напряжений, сопровождающийся появлением повышенных напряжений , на зажимах реактивных приемников и резким увеличением тока.

На схеме (рис.7-3) показан обрыв линейного провода А. В фазе ВС напряжения и тока сохраняются такими же , как в цепи без обрыва , а в фазах АВ и СА становятся обратными по отношению к схеме (рис.7-1).

Из схемы (рис.7-3) следует:

U_ВС=U_ВА + U_АС(7.10)

Фазы нагрузки АВи СА соединены последовательно , по этому фазные токи равны:

I_AB = I_CA

Применяя (7.7) к схеме (рис.7-3) , получим:

I_A= -I_AB - (-I_CA) = -I_AB + I_CA=0;

I_B= I_BC - (-I_AB) = I_BC + I_AB;(7.11)

I_C= -I_CA - I_BC = - ( I_BC + I_СА)= - I_B.

Векторная диаграмма (рис.7-2б) преобразуется для схемы (рис.7-3) в другую форму (рис.7-4).

Активная мощность однофазных приемников, соединенных треугольником, может быть выражена так

Р =U_ACI_Acos(U_AC^I_A)+U_BCI_Bcos(U_BC^I_B) (7.12)

Трехфазная цепь соединенная треугольником , является трехпроводной. В такой цепи , независимо от способа соединение потребителя , активная мощность может быть измеренна как алгебраическая сумма показаний двух ваттметров (рис.7-5)

P = P_W1 + P_W2(7.13)

Рис.7-3.Схема соединения потребителя треугольником с

оборванным линейным проводом А

Рис.7-4. Векторная диаграмма напряжений и токов при обрыве линейного провода А (несимметричная нагрузка)

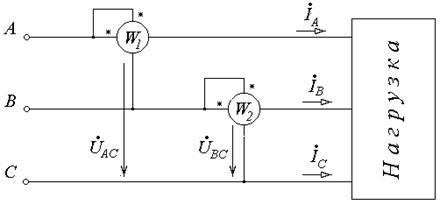
Рис.7-5 . Схема измерения активной мощности в трехфазной

сети с помощью двух ваттметров