Погрешности электрических измерений

Показание приборов всегда отличаются от действительных значений измеряемой величины. Оценка точности показаний определяется различными видами погрешности.

Абсолютная погрешность ∆А_x

Абсолютная погрешность ∆А_х показания прибора равна разности между показанием прибора А_х и действительным значением измеряемой величины А_д (рис.1-3)

∆А_х=А_х-А_д (1.1)

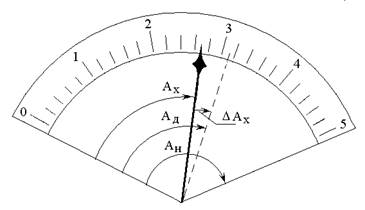
Рис.1-3

Основные величины на шкале:

А_х - показание прибора; А_д -действительное значение измеряемой величины; ∆А_х-абсолютная погрешность показания прибора; А_н-номинальное значение прибора (край шкалы).

Величина абсолютной погрешности в разных точках шкалы равная, она может быть и положительной, и отрицательной. Чем меньше абсолютная погрешность, тем достовернее результаты измерения.

Относительная погрешность- γ_х

Более общей и хорошо сопоставимой характеристикой измерения является относительная погрешность.

Относительная погрешность измерения равна отношению абсолютной погрешности измеряемой величины А_х к ее действительному значению А_д, выраженному в процентах (рис.1-3).

γ_х=∆Α_х/А_д· 100%≈ ∆A_х/A_x· 100% , (1.2)

так как А_д и А_х мало отличаются друг от друга.

Относительная приведенная погрешность-γ_пр

Погрешность самих приборов характеризуется величиной, называемой относительной приведенной погрешностью γ_пр.

Относительная приведенная погрешность равна отношению абсолютной погрешности прибора - ∆А_х к номинальному значению - А_н (т.е. к наибольшему значению, которое может быть измерено по шкале прибора), выраженному в процентах (рис.1-3).

γ_пр=∆А_х/А_н· 100% = (А_х-А_д)/А_н· 100% , (1.3)

где А_д- действительное значение измеряемой величины , отсчитываемое по эталонному прибору; А_х-соответствующее ему показание данного прибора.

Номинальное значение А_н многопредельных приборах определяется по максимальному значению шкалы; на которой производится измерение. Например, если амперметр имеет два предела на 1А и 2А , то номинальное значение на первом пределе будет А_н=1А , а на втором А_н=2А.

Класс точности прибора равен максимальному значению приведенной погрешности (1.3).

Согласно ГОСТу электроизмерительные приборы подразделяются на восемь классов точности (табл. 1-3).

Таблица 1-3

Однако класс точности прибора не определяет точность самого измерения. Чтобы доказать это , разделим и умножим выражение (1.2) на А_н , тогда

g_х=∆А_х/А_х·100· А_н/А_н= (∆А_х/А_н·100)· А_н/А_х,

согласно (1.3) имеем:

γ_х= γ_пр· А_н/А_х .

Полученное выражение показывает , что относительная погрешность измерения γ_х во столько раз больше класса точности прибора γ_пр, во сколько раз номинальное значение прибора А_н больше измеряемого значения А_х. При измерении электрических величин, близких к номинальному значению прибора (А_х»А_н), относительная погрешность измерения g_х приближается к классу точности прибора g_пр, а при измерении величин, малых по сравнению с номинальным значением прибора А_н, g_х может быть во много раз больше класса точности прибора.

Пример. Вольтметром класса 1,0 с номинальным значением U_н=250В измеряют напряжение U₁=50В и U₂=200В.

В первом случае погрешность измерения будет:

g₁= g_пр·U_н/U₁=1,0·250/50=5%

Во втором случае:

γ₂= γ_пр·U_н/U₂=1,0·250/200=1,25%

Поэтому для повышения точности измерения следует пользоваться приборами, у которых измеряемая величина отсчитывалась бы во второй половине шкалы. Это позволяет осуществлять измерения с погрешностью, не превышающей удвоенного значения класса точности прибора.