СРОК СЛУЖБЫ СШН
Срок службы насоса – время, прошедшее от спуска в скважину до момента, когда его дальнейшая эксплуатация становится нецелесообразной из-за низкой подачи.
Аналитический срок службы можно подсчитать по формуле Адонина-Пирвердяна:
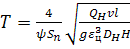 (283)
(283)
где  – параметр функции износа (по графику рисунок 75)
– параметр функции износа (по графику рисунок 75)
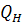 - начальная производительность, м3/сут;
- начальная производительность, м3/сут;
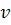 - вязкость жидкости, м2/с;π
- вязкость жидкости, м2/с;π
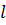 - длина плунжера, м;
- длина плунжера, м;
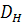 – диаметр плунжера, м;
– диаметр плунжера, м;
Н – напор, создаваемый насосом, м;
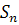 - длина хода, м;
- длина хода, м;
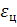 - износ цилиндра.
- износ цилиндра.
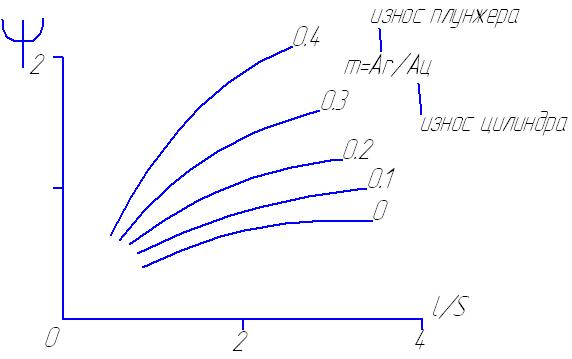
Рисунок 75 – График для определения параметра износа
Из формулы (283) следует, что продолжительность работы насоса вплоть до прекращения подачи зависит от следующих факторов:
а) износостойкости (или износа плунжера и цилиндра, характеризуемых коэффициентами Ац и 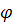 ; б) длины плунжера
; б) длины плунжера 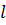 ; режима откачки, т.е. значений
; режима откачки, т.е. значений 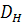 ,
, 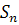 , n; г) условий эксплуатации – кинематической вязкости откачиваемой жидкости
, n; г) условий эксплуатации – кинематической вязкости откачиваемой жидкости 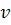 и высоты подъема (напора) жидкости Н.
и высоты подъема (напора) жидкости Н.
Оценка каждого из этих факторов может быть произведена, если мы зададимся одним из них для двух сравниваемых насосов, предположив все остальные данные одинаковыми.
Например, если мы хотим оценить влияние износостойкости цилиндров двух насосов на продолжительность их работы в скважине при прочих равных условиях, заранее условимся, что износостойкость цилиндра насоса 2 меньше износостойкости насоса 1 в 2 раза, т.е.
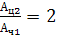 .
.
Кроме того примем, что  и
и  ;
; 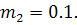
По графику (рисунок 75) находим значения 𝜓для каждого из насосов n, подставив их в формулу 274, получим:
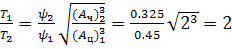
Следовательно, продолжительность работы насоса с более прочным цилиндром (в нашем примере насос 1) в 2 раза выше.
Ну а как влияет длина плунжера на срок работы насоса. Очевидно, формула 274 примет вид
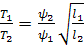
Приняв длину плунжера насоса 1 вдвое большей, чем у насоса 2,  для насоса 1,
для насоса 1, 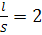 для насоса 2; m1=0.1 - одинаковый для обоих насосов получим по графику:
для насоса 2; m1=0.1 - одинаковый для обоих насосов получим по графику: 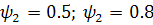

Дата добавления: 2015-04-15; просмотров: 1128;
