Парная корреляция

Парная корреляция позволяет оценить тесноту связи между двумя признаками. Для выявления корреляционной связи между двумя признаками можно построить поле корреляции.

Поле корреляции - это поле точек, координаты которых (х; у) определяются значениями факторного и результативного признаков.

Расположение точек на поле корреляции позволяет судить о наличии и о характере связи (нелинейная, а если линейная, то и о направлении (прямая или обратная)).

На рис. 1.1 показаны основные возможные способы расположения точек поля корреляции. Если точки поля корреляции располагаются в определенном направлении, то можно предположить наличие связи.

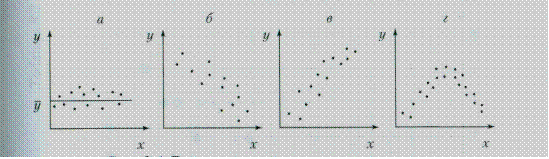
Рис. 1.1. Возможное расположение точек поля корреляции (х; у):

а – корреляция отсутствует; б – корреляция линейная обратная;

в – корреляция линейная прямая; г - корреляция нелинейная.

Пример 1.1. Изучается зависимость оценки, полученной на экзамене (у) 8 студентами, от суммы баллов (х), набранных ими в течение семестра. Данные приведены в табл. 1.1.

Таблица 1.1

Исходные данные

Для построения поля корреляции в координатных осях:

- на оси Х отложим значения баллов х, набранных студентами в течение семестра;

- на оси У покажем значения оценки у, полученной на экзамене студентами;

- нанесем точки с координатами (х; у) для каждого студента.

На рис. 1.2 показано поле корреляции. Расположение точек позволяет предположить, что существует прямая линейная связь между оценкой, полученной на экзамене (у) студентами, и суммой баллов (х), полученных ими в течение семестра.

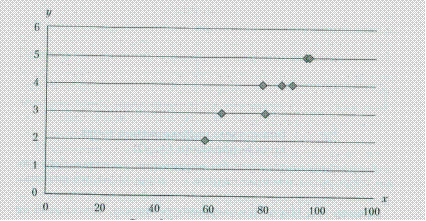
Рис. 1.2. Поле корреляции

Теснота линейной связи измеряется коэффициентом парной корреляции:

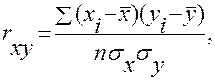
где - число наблюдений; - среднее квадратическое отклонение фактора х; - среднее квадратическое отклонение результата у. Или .

Если знаки отклонений от средних совпадают, то связь прямая ,

если знаки отклонений не совпадают, то связь обратная .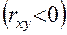

Величина коэффициента парной корреляции изменяется от -1 (полная обратная связь) до 1 (полная прямая связь):

.

Чем ближе значение 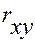к единице, тем связь теснее, чем ближе значение 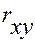к нулю, тем она слабее.

Коэффициент корреляции - это симметричная мера связи, т.е. это мера взаимосвязи между х и у. Поэтому .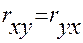

Характеризовать тесноту связи поможет следующая таблица:

Коэффициент корреляции	Характеристика связи
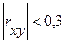
	Слабая
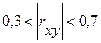
	Средняя
	Сильная или тесная

По данным примера табл. 1.1 рассчитаем коэффициент парной корреляции между оценкой (у), полученной на экзамене студентами, и суммой баллов (х), полученных ими в течение семестра:

- вычислим средние значения признаков:

- вычислим средние квадратические отклонения признаков и ,

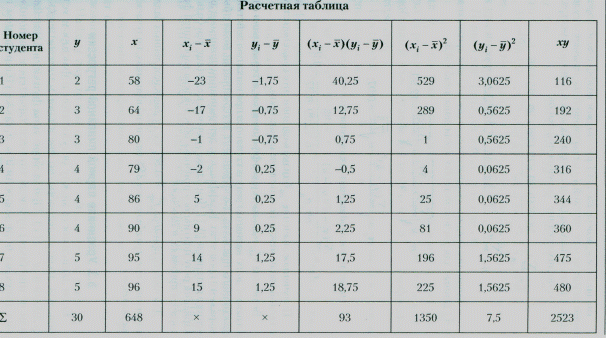
данные для расчета которых приведены в табл. 1.2:

- вычислим коэффициент корреляции:

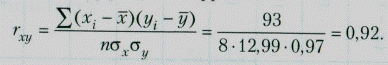
Таблица 1.2

Полученное значение 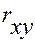близко к единице, что свидетельствует о тесной связи между результатом и фактором.

Величина называется коэффициентом детерминации и показывает долю вариации результативного признака под действием факторного признака. Коэффициент детерминации может быть выражен в процентах. Коэффициент детерминации принимает значения в интервале [0; 1]. Чем ближе значение к единице, тем больше вариация результативного признака обусловлена вариацией факторного признака, и наоборот.

Для нашего примера = 0,85, т.е. сумма накопленных баллов течение семестра объясняет 85% различий в оценках, получаемых на экзамене.