Кластеризация и квантование

Записав правило соревновательного обучения в градиентном виде: , легко убедиться, что оно минимизирует квадратичное отклонение входных векторов от их прототипов - весов нейронов-победителей:

.

Иными словами, сеть осуществляет кластеризацию данных: находит такие усредненные прототипы, которые минимизируют ошибку огрубления данных. Недостаток такого варианта кластеризации очевиден - "навязывание" количества кластеров, равного числу нейронов. В идеале сеть сама должна находить число кластеров, соответствующее реальной кластеризации векторов в обучающей выборке. Адаптивный подбор числа нейронов осуществляют несколько более сложные алгоритмы, такие, например, как растущий нейронный газ.

Идея последнего подхода состоит в последовательном увеличении числа нейронов-прототипов путем их "деления". Общую ошибку сети можно записать как сумму индивидуальных ошибок каждого нейрона:

.

Естественно предположить, что наибольшую ошибку будут иметь нейроны, окруженные слишком большим числом примеров и/или имеющие слишком большую ячейку. Такие нейроны и являются, в первую очередь, кандидатами на "почкование" (см. Рисунок 18).

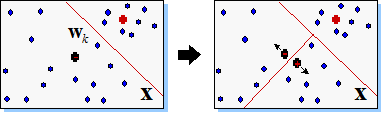
Рисунок 18. Деление нейрона с максимальной ошибкой в "растущем нейронном газе".

Соревновательные слои нейронов широко используются для квантования данных (vector quantization), отличающегося от кластеризации лишь большим числом прототипов. Это весьма распространенный на практике метод сжатия данных. При достаточно большом числе прототипов, плотность распределения весов соревновательного слоя хорошо аппроксимирует реальную плотность распределения многомерных входных векторов. Входное пространство разбивается на ячейки, содержащие вектора, относящиеся к одному и тому же прототипу. Причем эти ячейки (называемые ячейками Дирихле или ячейками Вороного) содержат примерно одинаковое количество обучающих примеров. Тем самым одновременно минимизируется ошибка огрубления и максимизируется выходная информация - за счет равномерной загрузки нейронов.

Сжатие данных в этом случае достигается за счет того, что каждый прототип можно закодировать меньшим числом бит, чем соответствующие ему вектора данных. При наличии прототипов для идентификации любого из них достаточно лишь бит, вместо бит описывающих произвольный входной вектор.