Конструктивные алгоритмы

Эти алгоритмы характеризуются относительно быстрым темпом обучения, поскольку разделяют сложную задачу обучения большой многослойной сети на ряд более простых задач, обычно - обучения однослойных подсетей, составляющих большую сеть. Поскольку сложность обучения пропорциональна квадрату числа весов, обучение “по частям” выгоднее, чем обучение целого:

.

Для примера опишем так называемую каскад-корреляционную методику обучения нейросетей. Конструирование сети начинается с единственного выходного нейрона и происходит путем добавления каждый раз по одному промежуточному нейрону (см. Рисунок 8).

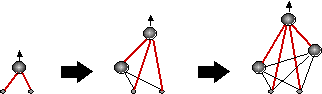
Рисунок 8.

Эти промежуточные нейроны имеют фиксированные веса, выбираемые таким образом, чтобы выход добавляемых нейронов в максимальной степени коррелировал с ошибками сети на данный момент (откуда и название таких сетей). Поскольку веса промежуточных нейронов после добавления не меняются, их выходы для каждого значения входов можно вычислить лишь однажды. Таким образом, каждый добавляемый нейрон можно трактовать как дополнительный признак входной информации, максимально полезный для уменьшения ошибки обучения на данном этапе роста сети. Оптимальная сложность сети может определяться, например, с помощью валидационного множества.

Bishop C.M. Neural Networks and Pattern Recognition. Oxford Press. 1995.

Fausett, L.V. Fundamentals of Neural Networks: Architectures, Algorithms and Applications. Prentice Hall, 1994.

Hertz, J., Krogh, A., and Palmer, R. Introduction to the Theory of Neural Computation. Addison-Wesley, 1991.

Masters,T. Practical Neural Network Recipes in C++. Academic Press. 1994.

McCord Nelson, M. and Illingworth, W.T. A Practical Guide to Neural Nets. Addison-Wesley, 1990.

Обучение без учителя: Сжатие информации

Прототипы задач: кластеризация данных, анализ главных компонент, сжатие информации. Хеббовское обучение. Автоассоциативные сети. Конкурентное обучение. Сети Кохонена. Гибридные архитектуры.

& … а мудрость его все возрастала, причиняя ему страдание полнотой своей.
Ф.Ницше, Так говорил Заратустра