Алгоритмы диагностирования

Составление алгоритмов диагностирования значительно упрощается, если при задании перечня дефектов указывается место конструкции, где возможен типовой дефект. Однако часто требуется найти место, где образовался дефект, и определить его причину. Причем если объект имеет только один дефект, то он называется одиночным. При нескольких дефектах говорят, что объект имеет кратный дефект. Если дефект не исчезает со временем, его называют константным, если же он самопроизвольно то появляется, то вновь исчезает – перемежающимся. Перемежающиеся дефекты наиболее характерны для электрооборудования, когда под действием вибрации вагона контакты (целостность цепи) то нарушаются, то вновь восстанавливаются.

По процедуре проведения проверок различают безусловный и условный алгоритмы диагностирования. Безусловный алгоритм диагностирования предопределяет выполнение проверок, в заранее фиксированном порядке, т. е. независимо от того, что вскрылось в процессе контроля. Условный алгоритм диагностирования предполагает, что каждая последующая проверка назначается в зависимости от исхода предыдущей проверки.

При характеристике алгоритма используются термины: с безусловной и с условной остановками. Алгоритмом с безусловной остановкой называется такой, когда диагноз составляется после выполнения всех проверок, предусмотренных алгоритмом.

Аналогично алгоритмом с условной остановкой называется такой, когда анализ результатов контроля выполняется после каждой проверки.

Пример 1.Диагностируемый блок электрооборудования вагона, который контролируется по безусловному алгоритму, показан на рис. 1.3.

N Х1 Х2 У

а б

Рис. 1.3 Диагностика блока электрооборудования
по безусловному алгоритму

Исходные положения следующие: входами блока являются Х₁и Х₂а выходом – У(рис. 1.3, а). Алгоритм диагностирования предусматривает три проверки N подачей единичного напряжения то на один Х₁ то на другой Х₂, то на оба входа. Результаты проверок исправного блока показаны на рис. 1.3, б. Например, при первой проверке подачей напряжения (N=1)на Х₂ результаты измерения на Х₂и Убудут равны 0.

Пусть теперь после второй проверки (N=2) реального блока результаты будут 1, 0, 1.Эти значения не совпадают с исправными 1, О, О(см. вторую строку рис. 1.3,6) и поэтому блок неисправен. Если диагноз составляется после получения всех значений выхода У, то алгоритм будет с безусловной остановкой, т. е. в этом случае выполнен весь процесс проверки и только тогда сформулирован диагноз.

Если сравнение номинальных и фактических значений выхода производится по мере их получения, то алгоритм является алгоритмом с условной остановкой. В последнем случае диагноз о неисправности элемента будет получен уже после подачи второго входного набора.

Блок исправен, если все полученные выходные значения совпадают с номинальными значениями.

Пример 2.Контроль по условному алгоритму проследим на проверке исправности выпрямителя в системе электрооборудования. Схема установки показана на рис. 1.4.

Рис. 1.4 Схема диагностирования выпрямителя системы электрооборудования

При контроле сначала на выпрямитель 1подается напряжение от аккумулятора 3через сигнальную лампу 2прямой полярности. Если лампа в этом случае не горит, то меняют полярность подаваемого на­пряжения от аккумулятора и при исправном выпрямителе лампа должна: загореться.

Пример 3. Рассмотрим пример построения рационального алгоритма диагностирования поиска элемента с пониженным сопротивлением изоляции в последовательной цепи, содержащей N_э=16 таких элементов. Алгоритм состоит в последовательном переборе и измерении сопротивления изоляции каждого элемента. При этом неисправный элемент может быть найден после случайного числа проверок, равного 1, 2, 3,..., 16.При равенстве вероятностей отказов элементов среднее число элементарных проверок, исключая определение, что цепь имеет где-то неисправность, равно (N_э+1)/2. Более рациональным является метод средней точки или метод половинного исключения. В этом случае при каждой элементарной проверке участок цепи делится на две группы, например по восемь элементов. Производится контроль первой группы из восьми элементов; если она исправна, то неисправность должна находиться в другой группе элементов. Вторую группу элементов из восьми элементов сразу же делят опять на две подгруппы по четыре элемента и измеряют исправность одной из подгрупп. Если подгруппа исправна, то неисправность находится в другой подгруппе. Опять подгруппу с неисправным; элементом делят надвое и т. д., пока методом исключения не находят неисправный элемент.

Математические методы

Применяемые в технической диагностике математические методы можно разделить на два больших класса: математическое моделирование диагностических процессов и применение различных теорий (теория распознавания образов, теория множеств и пр.). Наиболее эффективно применение математического моделирования при определении неисправностей в устройствах, содержащих электронные элементы. При диагностировании сложных динамических объектов, какими являются вагоны или ПС, использование математического моделирования затруднено из-за сложности определения аналитических зависимостей, связывающих внешние признаки и соответствующие им неисправности в деталях объекта. Тем не менее, использование математического моде­лирования позволяет расширить возможности диагностирования благодаря применению микропроцессорной вычислительной техники. Математическое моделирование позволяет сократить и удешевить процесс диагностирования, выбрать наиболее информативные диагностические параметры, проводить накопление информации в аналитической форме для прогнозирования техни­ческого состояния объекта.

При построении систем диагностирования большое распространение получили табличные (или матричные) алгоритмы, особенно если объект диагностирования имеет небольшой набор диагностических параметров. Чаще всего табличные алгоритмы применяются для предварительного диагноза, так как устройства диагностирования могут работать только по жесткой программе – детерминистской логике. Простота детерминистской логики во многих случаях не позволяет поставить достоверный диагноз, так как необходимым условием является полное совпадение диагностических параметров, при несоблюдении которого могут появиться признаки, отсутствующие в матрице. Табличные алгоритмы легко можно реализовать на релейных элементах, диодных матрицах или микропроцессорных устройствах.

Аналитические модели позволяют решать оптимизационные задачи и получать соотношения между состояниями объекта, диагностическими параметрами и показателями качества в аналитическом виде. Аналитическими моделями являются различные функции, связывающие между собой внешние и внутренние параметры элементов системы и выходные параметры вида
Z = y(x, y_нач, t). В процессе работы объекта изменяются внешние и внутренние параметры, а следовательно, происходит изменение выходных параметров. Решая функциональные уравнения зависимостей, можно выявить техническое состояние объекта в произвольный промежуток времени с учетом изменения внешних и внутренних параметров. Для реализации аналитических моделей технического состояния объекта наиболее перспективно использование микропроцессорных устройств.

При разработке математической диагностической модели необходимо учитывать вероятность появления отказов и законы распределения отказов по времени работы или по пробегу ПС. Для решения данной задачи необходимо использовать вероятностные алгоритмы, основанные на вероятности возникновения определенных дефектов при наличии определенных диагностических параметров. Часто для определения возникновения дефектов пользуются формулой Байеса:

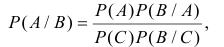
где Р(А/В) – вероятность того, что при наличии суммы диагностических параметров В имеется дефект А.

Р(А) – вероятность дефекта А при случайном выборе диагностических па­раметров;

Р (В/А) – известная из опыта вероятность наличия суммы диагностических параметров В при возникновении дефекта;

Р(С)Р(В/С) – сумма произведений вероятностей каждого из рассматривае­мых дефектов па вероятности данной суммы признаков каждого из дефектов.

Таким образом, существует возможность формализовать логический процесс анализа дефектов при несовпадении всех диагностических параметров по вероятностному алгоритму.

Метод граф-моделей основан на использовании теорий отношений и теории графов. Применение этого метода позволяет значительно сократить объем вычислений при достаточной точности решения. Задачу технической диагностики, связанную с построением программы поиска неисправностей и контроля работоспособности, можно отнести к задачам математического программирования. Одним из вариантов решения задач математического программирования является метод «ветвей и границ». Преимущество данного метода заключается в том, что для него не требуется точных количественных соотношений между параметрами. Топологическая модель позволяет описать работу сложного объекта в целом и дает возможность легкого построения модели в случае конструктивных изменений в объекте.

Для решения логических задач технического диагностирования иногда наиболее эффективной оказывается теории распознавания образов. Под термином «образ» подразумевается совокупность воспринимаемых параметров объекта или явлений, принадлежащих одному классу. Параметры образа могут изменяться, тогда как образ будет относиться к одному и тому же классу. Задача теории состоит в том, чтобы построить узнающую систему, которая бы по описанию произвольного объекта из начального множества устанавливала его при­надлежность к соответствующему классу. Техническую диагностику можно считать частным случаем теории распознавания образов, согласно которой сначала устанавливаются варианты различаемых состояний, а затем выбирают такие признаки, по которым можно судить о том, какой из установленных вариантов состояния имеет в данный момент диагностируемый объект.

Частным случаем решения задачи распознавания образов является задача распознавания размытых множеств. Обнаружение дефектов в объекте с использованием теории размытых множеств осуществляется следующим образом: составляется граф-модель и проводится предварительная минимизация числа точек снятия диагностической информации; определяется значение контролируемых параметров; определяются техническое состояние и значение функций принадлежности к заранее составленному перечню классов состояний; определяется класс состояний, соответствующий неизвестной входной ситуации, поиском наибольшей степени разделимости классов. Задачи распознавания образов решаются в основном с использованием микропроцессорных устройств.