Правило обучения Ойа

От этого недостатка, однако, можно довольно просто избавиться, добавив член, препятствующий возрастанию весов. Так, правило обучения Ойа:

, или в векторном виде: ,

максимизирует чувствительность выхода нейрона при ограниченной амплитуде весов. В этом легко убедиться, приравняв среднее изменение весов нулю. Умножив затем правую часть на , видим, что в равновесии: . Таким образом, веса обученного нейрона расположены на гипер-сфере: .

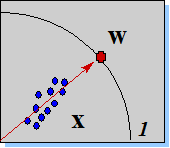
Рисунок 11. При обучении по правилу Ойа, вектор весов нейрона располагается на гипер-сфере в направлении, максимизирующем проекцию входных векторов.

Отметим, что это правило обучения по существу эквивалентно дельта-правилу, только обращенному назад - от входов к выходам (т.е. при замене ). Нейрон как бы старается воспроизвести значения своих входов по заданному выходу. Тем самым, такое обучение стремится максимально повысить чувствительность единственного выхода-индикатора к многомерной входной информации, являя собой пример оптимального сжатия информации.

Эту же ситуацию можно описать и по-другому. Представим себе персептрон с одним (здесь - линейным) нейроном на скрытом слое, в котором число входов и выходов совпадает, причем веса с одинаковыми индексами в обоих слоях одинаковы. Будем учить этот персептрон воспроизводить в выходном слое значения своих выходов. При этом, дельта-правило обучения верхнего (а тем самым и нижнего) слоя примет вид правила Ойа:

.

Рисунок 12. Автоассоциативная сеть с узким горлом - аналог правила обучения Ойа

Таким образом, существует определенная параллель между самообучающимися сетями и т.н. автоассоциативными сетями, в которых учителем для выходов являются значения входов. Подобного рода нейросети с узким горлом также способны осуществлять сжатие информации.

Взаимодействие нейронов: анализ главных компонент

Единственный нейрон осуществляет предельное сжатие многомерной информации, выделяя лишь одну скалярную характеристику многомерных данных. Каким бы оптимальным ни было сжатие информации, редко когда удается полностью охарактеризовать многомерные данные всего одним признаком. Однако наращиванием числа нейронов можно увеличить выходную информацию. В этом разделе мы обобщим найденное ранее правило обучения на случай нескольких нейронов в самообучающемся слое, опираясь на отмеченную выше аналогию с автоассоциативными сетями.