Fig.2.3 A ship as a dynamic control system
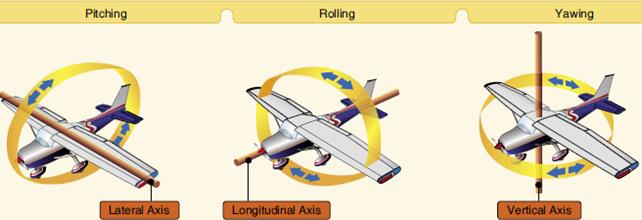
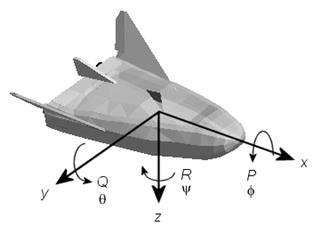
An aircraft’s angles of rotation
Rotations are defined by the Euler angles P, Q, R or Φ, Θ, Ψ.
They are:
| P or Φ | Roll about the x-axis |
| Q or Θ | Pitch about the y-axis |
| R or Ψ | Yaw about the z-axis |
We may consider some object (say, ship) as a dynamic control system with
the following control input signals:
- rudder’s position;
- engines’ output;
- wind speed;
control output signals:
- a position;
- forward velocity;
- a heading;
- ship motion (pitching, rolling, yawing).
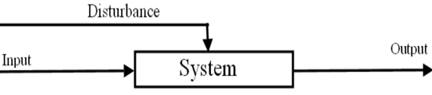
A control system is an interconnection of components forming a system configuration that will provide a desired system response. The basis for analysis of a system is the foundation provided by linear system theory, which assumes a cause-effect relationship for the components of a system. Therefore a component or process to be controlled can be represented by a block, as shown in Figure 3. The input–output relationship represents the cause-and-effect relationship of the process, which in turn represents a processing of the input signal to provide an output signal variable, often with a power amplification.
In the case if some control system has inertial properties then the change in its output coordinates won’t be instant. This controlled object will have dynamic properties.
The change in output coordinates of some controlled process is defined by the aggregate of rules or mathematical relations called system functional algorithm.
Using the established system’s functional algorithm we may define system control algorithm which ensures the execution of the mentioned functional algorithm with required accuracy.
There are 3 fundamental control principles:
- open-loop control;
- feed-forward control;
- feedback control.
We must also mention that you may meet in practice the combination of the mentioned control principles.
- Open-loop control.
Дата добавления: 2015-03-09; просмотров: 1271;
