Решение. Выберем основную систему, отбросив левое закрепление и приложив реактивные силы (лишние неизвестные) Х1
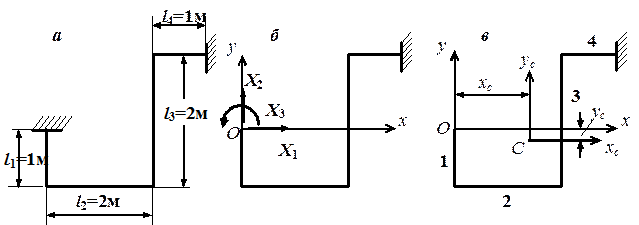 Рис. 4.48. К примеру расчета трубопровода: а – заданная система;
б – основная система;
в – положение упругого центра
Рис. 4.48. К примеру расчета трубопровода: а – заданная система;
б – основная система;
в – положение упругого центра
|
Выберем основную систему, отбросив левое закрепление и приложив реактивные силы (лишние неизвестные) Х1, Х2 и Х3 (рис. 4.48, б). Для определения значений лишних неизвестных по формулам (4.30) – (4.32) найдем сначала положение упругого центра и геометрические характеристики 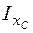 ,
, 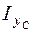 и
и 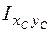 .
.
Координаты упругого центра в системе координат xОy сосчитаем по формулам (4.33), где
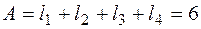 м.
м.
Статический момент относительно оси х равен сумме статических моментов четырех прямоугольников единичной толщины:
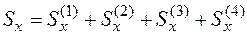 .
.
Статический момент третьего участка трубопровода (третьего прямоугольника) 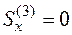 , так как центр тяжести этого прямоугольника лежит на оси х, а статические моменты остальных прямоугольников найдем следующим образом:
, так как центр тяжести этого прямоугольника лежит на оси х, а статические моменты остальных прямоугольников найдем следующим образом:
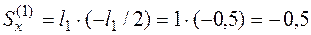 м2,
м2,
где 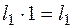 – площадь первого прямоугольника, а (–
– площадь первого прямоугольника, а (– 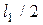 ) – координата центра тяжести. Аналогично
) – координата центра тяжести. Аналогично
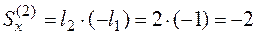 м2,
м2,
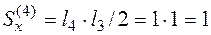 м2.
м2.
Таким образом,
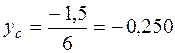 м.
м.
Вторая координата упругого центра
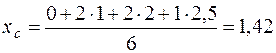 м.
м.
Отложим эти координаты на рисунке и покажем точку С – упругий центр. Проведем через точку С центральные оси xc, yc (рис. 4.48, в). Найдем моменты инерции фигуры относительно этих осей. Момент инерции относительно оси хс равен сумме моментов инерции четырех прямоугольников:
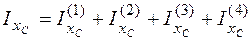 .
.
Сосчитаем момент инерции первого прямоугольника относительно оси хс по формуле (4.34). Для рассматриваемого прямоугольника собственная ось х0 перпендикулярна стороне l1, поэтому первый член в (4.34) (момент инерции первого прямоугольника собственной оси х0 ) не равен нулю. Таким образом, момент инерции относительно оси хс
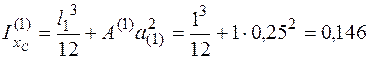 м3.
м3.
Для второго прямоугольника момент инерции относительно
оси хс
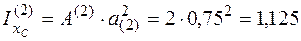 м3.
м3.
Поскольку ось х0 параллельна стороне прямоугольника l2, то первое слагаемое в формуле (4.34) отсутствует ( 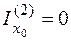 ). Аналогично находим моменты инерции остальных прямоугольников:
). Аналогично находим моменты инерции остальных прямоугольников:
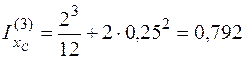 м3;
м3;
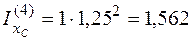 м3.
м3.
И полный момент инерции относительно оси хс равен  м3. Так же вычислим момент инерции относительно оси yc каждого прямоугольника:
м3. Так же вычислим момент инерции относительно оси yc каждого прямоугольника:
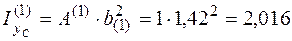 м3;
м3;
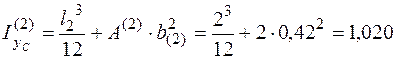 м3;
м3;
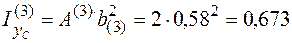 м3;
м3;
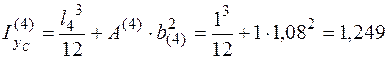 м3.
м3.
Полный момент инерции относительно оси yc равен сумме моментов инерции всех прямоугольников 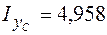 м3.
м3.
Найдем центробежный момент инерции. Момент инерции каждого прямоугольника определим по формуле (4.36). Обратим внимание на то, что, если при вычислении осевых моментов инерции знаки координат а и b можно опускать, так как они входят в формулы (4.34), (4.35) в квадрате, то при вычислении центробежного момента инерции эти знаки следует обязательно учитывать. Тогда
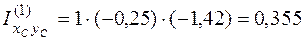 м3;
м3;
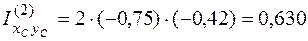 м3;
м3;
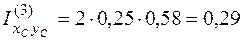 м3;
м3;
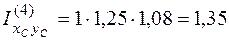 м3.
м3.
Полный центробежный момент инерции 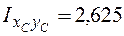 м3.
м3.
Длины трубопровода вдоль осей х и y: 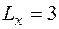 м,
м, 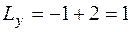 м. Подставляя найденные геометрические характеристики в формулы (4.30)–(4.32), сосчитаем значения лишних неизвестных:
м. Подставляя найденные геометрические характеристики в формулы (4.30)–(4.32), сосчитаем значения лишних неизвестных:
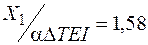 м–2;
м–2;
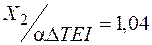 м–2;
м–2;
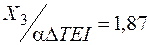 м–1.
м–1.
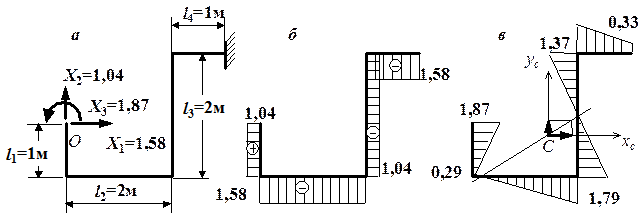 Рис. 4.49. Определение внутренних усилий в трубопроводе:
а – основная система с найденными реакциями в долях от aDTЕI;
б – эпюра продольных сил N в долях от aDTЕI;
в – эпюра изгибающих моментов М в долях от aDTЕI
Рис. 4.49. Определение внутренних усилий в трубопроводе:
а – основная система с найденными реакциями в долях от aDTЕI;
б – эпюра продольных сил N в долях от aDTЕI;
в – эпюра изгибающих моментов М в долях от aDTЕI
|
Нарисуем основную систему и приложим в точке О найденные опорные реакции. Так как все лишние неизвестные оказались положительными, то сохраняем выбранное ранее направление всех неизвестных (рис. 4.49, а). Построим эпюры продольных сил и изгибающих моментов в долях от 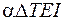 (рис. 4.49, б, в). На рис. 4.49, в показана равнодействующая сил Х1 и Х2, приложенных в упругом центре. Видно, что на линии действия этой равнодействующей изгибающий момент равен нулю.
(рис. 4.49, б, в). На рис. 4.49, в показана равнодействующая сил Х1 и Х2, приложенных в упругом центре. Видно, что на линии действия этой равнодействующей изгибающий момент равен нулю.
Теперь можно решать вопрос о проверке прочности трубы. По эпюрам N и М находим опасное сечение. У нас это сечение в точке О (рис. 4.49, а). [14] В этом сечении действуют одновременно максимальный изгибающий момент и растягивающая продольная сила: 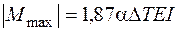 ,
, 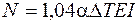 . Напряжения в опасных точках вычисляем по формулам (4.37) и (4.38). Для удобства расчетов приведем формулу (4.37) к другому виду. Максимальное напряжение от изгиба
. Напряжения в опасных точках вычисляем по формулам (4.37) и (4.38). Для удобства расчетов приведем формулу (4.37) к другому виду. Максимальное напряжение от изгиба
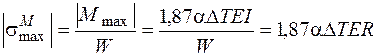 ,
,
так как момент сопротивления 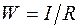 . Нормальное напряжение, вызванное продольной силой, найдем так:
. Нормальное напряжение, вызванное продольной силой, найдем так:
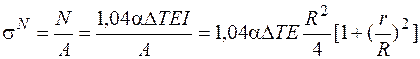 ,
,
где учтено, что для трубы
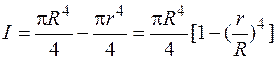 ,
, 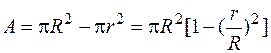 ,
,
r – внутренний радиус трубы. Суммарные напряжения на площадках, перпендикулярных оси х, находим согласно (4.37), складывая sN и 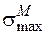 .
.
Отметим особенность решаемой задачи об определении температурных напряжений в статически неопределимой раме: чем больше размер поперечного сечения (больше радиус трубы), тем больше возникающие в конструкции температурные напряжения. Это связано с тем, что с увеличением радиуса увеличивается жесткость рамы и уменьшается свобода деформаций, что и приводит к увеличению напряжений.
Вычисляя напряжения в опасных точках, обратите внимание на единицы измерения величин, входящих в формулы для напряжений. В формуле для определения 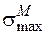 число 1,87 имеет размерность м–1, в формуле для
число 1,87 имеет размерность м–1, в формуле для 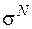 число 1,04 измеряется в м–2. Таким образом, подставляя R в метрах, получим величину напряжения в тех же единицах измерения, что и модуль упругости Е. При проверке прочности в опасных точках трубы используйте знания, полученные при изучении разд. 2 "Исследование плоского напряженного состояния. Проверка прочности для сложного напряженного состояния" [5]. Если условие прочности выполняться не будет, следует уменьшить радиус трубы и добиться удовлетворения условия прочности.
число 1,04 измеряется в м–2. Таким образом, подставляя R в метрах, получим величину напряжения в тех же единицах измерения, что и модуль упругости Е. При проверке прочности в опасных точках трубы используйте знания, полученные при изучении разд. 2 "Исследование плоского напряженного состояния. Проверка прочности для сложного напряженного состояния" [5]. Если условие прочности выполняться не будет, следует уменьшить радиус трубы и добиться удовлетворения условия прочности.
Дата добавления: 2015-03-07; просмотров: 670;
