Решение. Рассматриваемая рама является один раз статически неопределимой и для выбора основной системы требуется отбросить одну лишнюю связь
Рассматриваемая рама является один раз статически неопределимой и для выбора основной системы требуется отбросить одну лишнюю связь. Такой лишней связью будем считать шарнирно-
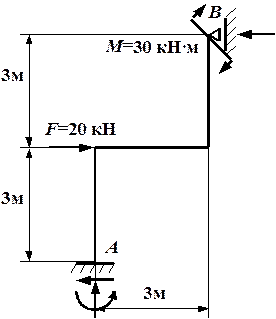Рис. 4.40. Схема рамы с нагрузками
|
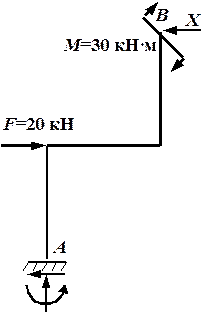Рис. 4.41. Основная система
|
подвижную опору в точке В. Основная система с отброшенной лишней связью показана на рис. 4.41. Лишняя неизвестная, то есть реакция в отброшенной лишней связи, обозначена буквой Х. Условие совместности деформаций для выбранной основной системы – это условие, приравнивающее нулю горизонтальное перемещение точки В: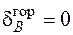 
. Это перемещение складывается из перемещения, вызванного всей заданной нагрузкой 
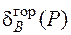, и перемещения от лишней неизвестной 
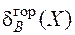. Тогда условие совместности деформаций запишем так:
.
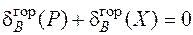Будем искать перемещения методом Максвелла – Мора с использованием правила Верещагина. Для этого построим три эпюры изгибающих моментов в основной системе: от заданной нагрузки (рис. 4.42, а), от единичной силы, соответствующей горизонтальному перемещению в точке В (рис. 4.42, б), и от лишней неизвестной Х (рис. 4.42, в). Для определения 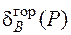перемножим эпюры МР и М1:
.
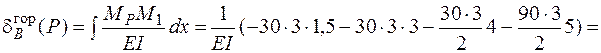
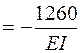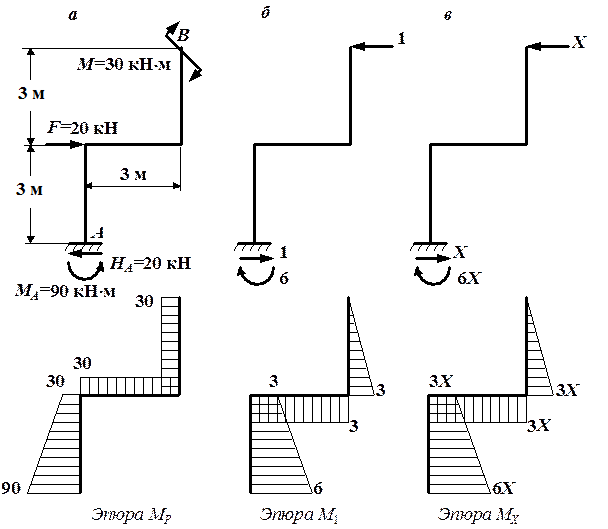Рис. 4.42. Эпюры изгибающих моментов: а – от заданной нагрузки;
б – от единичной силы; в – от лишней неизвестной Х
|
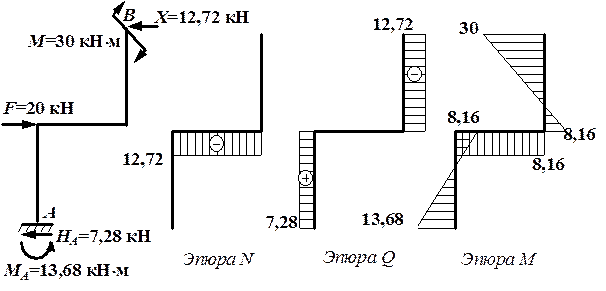Рис. 4.43. Окончательные эпюры внутренних усилий
|
Горизонтальное перемещение точки В от лишней неизвестной Х
.
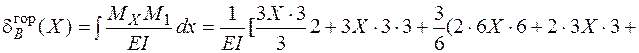
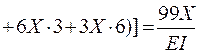Подставим найденные перемещения в условие совместности деформаций и найдем значение лишней неизвестной:
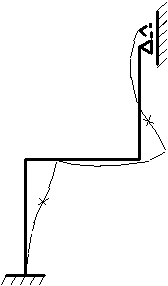Рис. 4.44. Изогнутая ось рамы
|
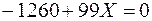, откуда 
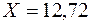кН.
Строим окончательные эпюры внутренних усилий, приложив к основной системе все нагрузки, включая найденное значение Х (рис. 4.43). Выполним проверку, перемножив эпюру М с эпюрой М1.
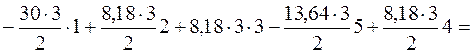
=147,24 – 147,3 » 0.
Изогнутая ось рамы, соответствующая эпюре изгибающих моментов (рис. 4.43, г), и условиям закрепления показана на рис. 4.44. Крестиками на рисунке отмечены точки перегиба оси.
Дата добавления: 2015-03-07; просмотров: 609;