Решение. Для определения перемещений балки аналитическим способом составим дифференциальное уравнение изогнутой оси (4.16)

Для определения перемещений балки аналитическим способом составим дифференциальное уравнение изогнутой оси (4.16), используя правила Клебша записи выражения для изгибающего момента. Начало координат в рассматриваемой задаче рациональнее выбрать справа (в заделке). Распределенную нагрузку 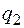, которая не доходит до левого конца балки, продлим до сечения С (рис. 4.20, в). Выражение для изгибающего момента будет иметь такой вид:

.

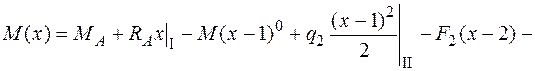
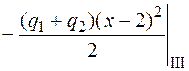Подставим это выражение в дифференциальное уравнение (4.16) и проинтегрируем его два раза:

;

;

.

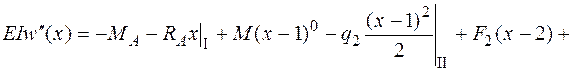
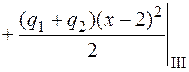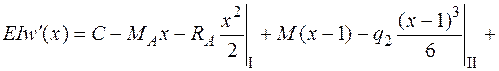
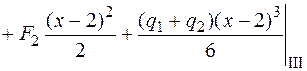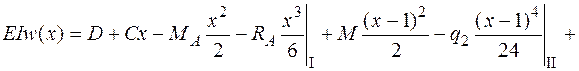
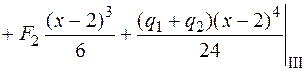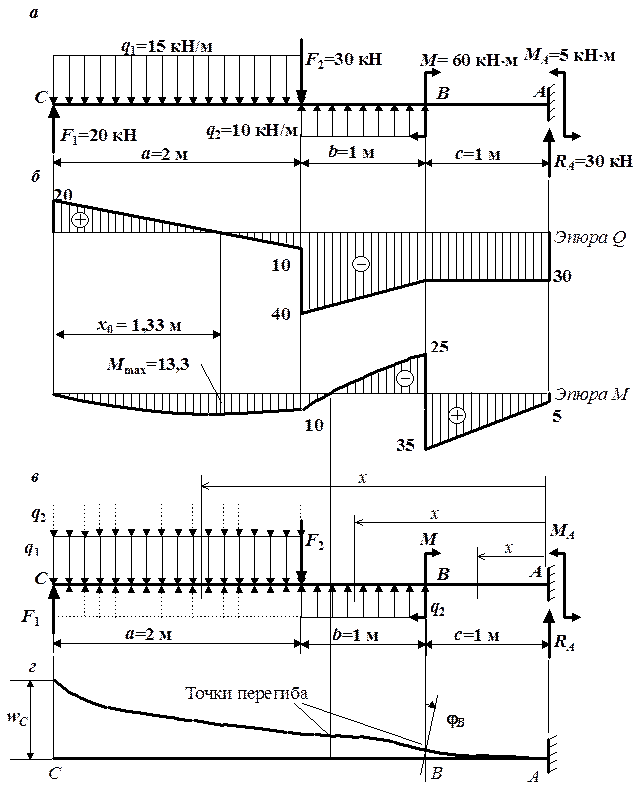Рис. 4.20. К решению примера 1 аналитическим способом: а – схема балки с нагрузками; б) эпюры Q и М; в – иллюстрация правил Клебша; г – изогнутая ось балки

Для определения постоянных С и D запишем граничные условия: в заделке (в сечении А, где находится начало координат) угол поворота и прогиб балки равны нулю, то есть

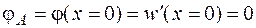и .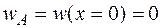

Подставляя эти условия в выражения для угла поворота и прогиба на первом участке, найдем, что

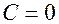и .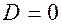

Теперь можно определить заданные перемещения. Для определения угла поворота в сечении В подставим в выражение для угла поворота на первом участке (только до черты с номером I) значение :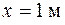

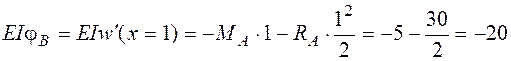кН×м².

В соответствии с правилом знаков отрицательный знак угла поворота для выбранного начала координат х справа означает, что поворот сечения происходит по часовой стрелке.

В сечении С, где требуется найти прогиб, координата х равна 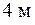, и это сечение находится на третьем участке балки, поэтому подставляем х = 4 м в выражение для прогибов, используя слагаемые на всех трех участках:

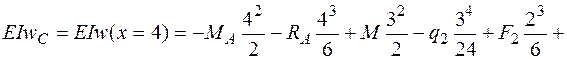
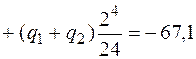кН·м³.

Знак минус у найденного прогиба показывает, что сечение С перемещается вверх. Покажем найденные перемещения на изогнутой оси балки. Чтобы нарисовать ось балки после деформации, построим эпюру изгибающих моментов (рис. 4.20, б). Положительный знак эпюры М на участке показывает, что балка на этом участке изгибается выпуклостью вниз, при отрицательном знаке М изогнутая ось имеет выпуклость вверх. Кроме того, деформированная ось балки должна удовлетворять условиям закрепления: в нашем случае на правом конце балка имеет жесткое защемление, и, как уже отмечалось при записи граничных условий, прогиб и угол поворота в защемлении должны равняться нулю. На рис. 4.20, г изображена ось рассматриваемой балки после деформации, удовлетворяющая этим условиям. На изогнутой оси показаны найденные прогиб в сечении С и угол поворота сечения В с учетом их знаков.

В заключение сосчитаем прогиб балки в сантиметрах, угол поворота в радианах и проверим условие жесткости. Найдем жесткость ЕI рассматриваемой деревянной балки из трех бревен радиусом 12 см. Момент инерции поперечного сечения

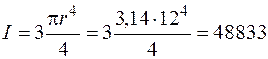см⁴.

Модуль упругости дерева Е = 10⁴ МПа = 10³ кН / см². Тогда

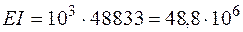кН·см².

Прогиб балки в сечении С

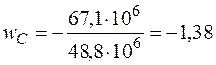см,

а угол поворота сечения В

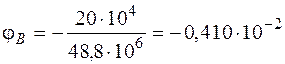рад.

Очевидно (см. рис. 4.20, г), что найденный прогиб балки в сечении С является максимальным, поэтому для проверки условия жесткости сравним его с допускаемым прогибом. Для балки длиной 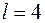м допускаемый прогиб согласно условию 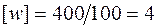см. Таким образом, максимальный прогиб 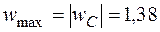см меньше допускаемого, и условие жесткости выполняется.