Метод Максвелла – Мора определения перемещений

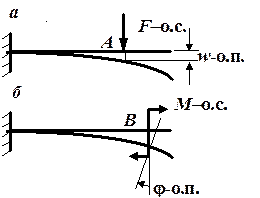Рис. 4.17. Два варианта обобщенных сил и соответствующих им обобщенных перемещений

Метод Максвелла – Мора определения перемещений является универсальным методом, справедливым, в отличие от рассмотренного выше аналитического способа, не только для балок, но и для любых стержневых систем. Чтобы понять сущность метода Максвелла – Мора, введем понятия обобщенной силы и обобщенного перемещения [2]. Обобщенной силой называется любое однопараметрическое силовое воздействие: это может быть и сосредоточенная сила, и сосредоточенный момент, и распределенная нагрузка, и группа сил, связанных между собой. Обобщенным перемещением, соответствующим заданной обобщенной силе, называется то перемещение, на котором обобщенная сила совершает работу. Приведем два самых важных для практики примера. Если обобщенной силой (о.с.) является вертикальная сосредоточенная сила, приложенная в точке А балки, то соответствующим этой силе обобщенным перемещением (о.п.) является перемещение по направлению этой силы, то есть прогиб в точке А (рис. 4.17, а), так как именно на таком перемещении сила F совершает работу. Если обобщенной силой является сосредоточенная пара сил, приложенная в точке В, то обобщенным перемещением, соответствующим этой обобщенной силе, будет угол поворота в сечении В (рис. 4.17, б).

Запишем приближенную формулу Максвелла – Мора, которая используется для определения перемещений в изгибаемых плоских стержневых системах и не учитывает влияния на перемещения продольной и поперечной сил:

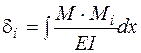. (4.21)

В этой формуле 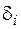– искомое обобщенное перемещение (это может быть и прогиб, и угол поворота любого сечения); М – изгибающий момент от заданной нагрузки; М_i – изгибающий момент, вызванный единичной обобщенной силой, соответствующей искомому перемещению; EI – жесткость стержня при изгибе (произведение модуля упругости на момент инерции). Интегрирование в формуле Максвелла – Мора ведется по длинам всех стержней конструкции (по длинам всех участков балки).

Таким образом, чтобы воспользоваться формулой Максвелла – Мора, надо:

1) определить изгибающий момент на каждом участке от заданной нагрузки;

2) освободить конструкцию от заданной нагрузки и загрузить ее единичной обобщенной силой, соответствующей искомому перемещению, то есть:

· если мы хотим определить вертикальное перемещение какой-то точки, то в этой точке следует приложить сосредоточенную силу, положить ее равной единице и найти изгибающий момент, вызванный действием только этой силы;

· если требуется найти угол поворота какого-то сечения, то в этом сечении надо приложить сосредоточенную пару, равную единице, и найти изгибающий момент от этой пары;

3) подставить произведение изгибающих моментов от нагрузки и от единичной обобщенной силы в интеграл (4.21) и проинтегрировать по всей длине конструкции.

Введем правило знаковв методе Максвелла – Мора:полученный по формуле Максвелла – Мора положительный знак перемещения показывает, что искомое перемещение происходит по направлению, совпадающему с принятым направлением единичной обобщенной силы, отрицательный знак перемещения говорит о том, что точки оси перемещаются (сечения поворачиваются) в сторону, противоположную направлению единичной обобщенной силы.

Очень распространенным способом интегрирования формулы Максвелла – Мора является способ графического интегрирования, называемый правилом Верещагина. Для того, чтобы воспользоваться правилом Верещагина, надо построить графики функций М и 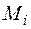, входящих в подынтегральное выражение формулы Максвелла – Мора. Такими графиками являются эпюры М и 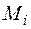. Операция интегрирования формулы Максвелла – Мора с помощью правила Верещагина носит название "перемножение эпюр". Правило Верещагина состоит в следующем:

1. Разбиваем эпюру М на простые фигуры, для которых известно положение центра тяжести (прямоугольники, треугольники и т. п.)[8].

2. Находим площади этих фигур 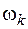. При определении площадей учитываем знаки ординат.

3. Под центрами тяжести этих фигур находим ординаты 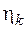на эпюре 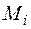(с учетом знаков).

4. Искомый интеграл будет равен (при постоянной жесткости балки 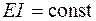) сумме произведений площадей 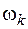на соответствующие им ординаты под центрами тяжести 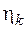, то есть

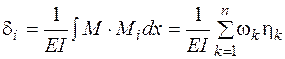, (4.22)

где n – количество фигур, на которые разбита эпюра М.

Примечание. Та эпюра (чаще всего 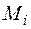), на которой ищем ординату под центром тяжести, должна быть обязательно линейна на всем участке перемножения.

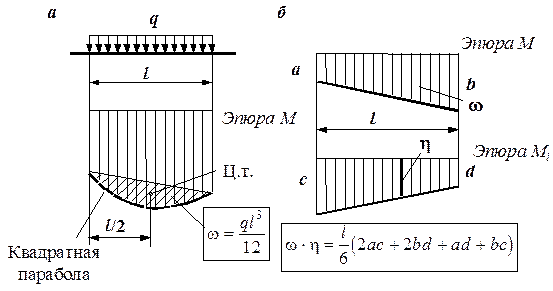Рис. 4.18. Некоторые полезные формулы для перемножения эпюр

В заключение приведем некоторые формулы, которые удобно использовать при перемножении эпюр. Если на участке балки действует равномерно распределенная нагрузка, то, как известно, эпюра изгибающих моментов на этом участке является квадратной параболой. Площадь сегмента, ограниченного квадратной параболой и показанного на рис. 4.18, а, вычисляется по формуле

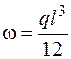, (4.23)

а центр тяжести этой фигуры находится посередине, независимо от угла наклона секущей. Если обе перемножаемые эпюры линейны и представляют собой трапеции (рис. 4.18, б), то, чтобы не разбивать эти трапеции на треугольники и прямоугольники, удобно воспользоваться формулой перемножения трапеций

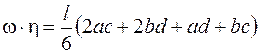, (4.24)

где ординаты a, b, c и d на эпюрах М и М_i показаны на рис. 4.18, б (берутся с учетом знаков); l – длина перемножаемого участка эпюр.

Рис. 4.19. Пояснения к формуле Симпсона

Вторым способом графического интегрирования формулы Максвелла – Мора является способ, использующий формулу Симпсона. Эта формула получена из известной в математике формулы Симпсона приближенного интегрирования путем деления участка интегрирования на два отрезка. Если подынтегральные функции М и М_i – линейные или квадратные параболы, то формула Симпсона дает точное значение интеграла. Приведем эту формулу, применяемую для перемножения эпюр,

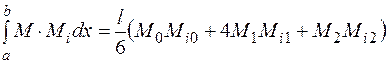. (4.25)

В написанной формуле 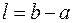– длина участка интегрирования; 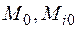и 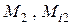– значения крайних ординат на эпюрах М и М_i; 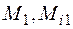– ординаты на эпюрах М и М_i, вычисленные в середине участка перемножения (рис. 4.19).