ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ. Различают три вида спектров излучения — линейчатые, полосатые и сплошные

Различают три вида спектров излучения — линейчатые, полосатые и сплошные. Линейчатые спектры наблюдаются в тех случаях, когда излучают отдельные атомы или ионы. Они состоят из ряда характерных для данного вещества линий, разделенных темными промежутками. Каждой линии соответствует определенная длина волны, называемая монохроматической. Линейчатые спектры характеризуют явления, происходящие внутри атома.

Полосатые спектры испускаются молекулами. Полоса представляет собой ряд близко расположенных спектральных линий. Излучение полосатых спектров свидетельствует об усложнении энергетических состояний молекулы по сравнению с состояниями изолированного атома, вследствие колебательного и вращательного движений составляющих ее ядер.

Сплошные спектры испускаются твердыми телами. Непрерывный характер этих спектров является следствием сильного взаимодействия частиц, составляющих твердое тело.

Вид линейчатого спектра зависит от строения атома соответствующего химического элемента, поэтому всем химическим элементам присущи строго определенные линейчатые спектры, отличающиеся друг от друга как числом линий, так и их длинами волн. Наиболее простой линейчатый спектр дает атом водорода, имеющий самое простое строение. Поиск объяснений закономерностей, присущих этому спектру, привело к созданию квантовомеханической теории атома.

Прежде всего следует отметить, что линии в спектре излучения любого атома, в том числе и атома водорода, расположены не беспорядочно, а могут быть объединены в группы, называемые сериями. Расположение линий в этих сериях подчинено определенным закономерностям. В видимой части спектра атома водорода это серия Бальмера, в ультрафиолетовой - серия Лаймана, в ближней инфракрасной — серия Пашена и т.д. Найденная опытным путем формула для длин волн l линий в каждой из этих серий имеет вид:

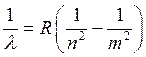. (1)

Ее называют обобщенной формулой Бальмера. В этой формуле R = 1,097×10⁷ м^-1 — постоянная Ридберга, n и m целые числа. При заданном n число m принимает все целочисленные значения, начиная с n + 1. Если n = 1 формула (1) описывает серию Лаймана, n = 2 серию Бальмера, n = 3 - серию Пашена.

Физический смысл этой формулы вытекает из теории строения атома водорода и водородоподобных атомов, созданной Бором на основе квантовой гипотезы Планка и классической планетарной модели атома Резерфорда. Основные положения развитой им теории Бор постулировал.

Первый постулат: в атоме существует ряд дискретных стационарных состояний, которым соответствуют определенные значения энергии атома: Е₁, Е₂, Е₃, … . В стационарном состоянии атом не излучает и не поглощает энергии.

Второй постулат: испускание и поглощение энергии происходит при переходе из одного стационарного состояния в другое. При этом испускается или поглощается квант энергии hn, равный разности энергий двух стационарных состояний:

hn = E_m - E_n (2)

где h — постоянная Планка. Выражение (2) определяет частоту n монохроматического излучения, испускаемого или поглощаемого атомом при переходе из состояния m в состояние n (условие частот Бора).

Дискретные стационарные состояния в теории Бора отбирались с помощью специального правила квантования орбит, которое формулировалось следующим образом: из всех возможных согласно классической механике орбит осуществляются только такие, на которых момент импульса электрона кратен величине 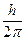(третий постулат):

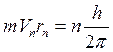. (3)

В формуле (3) m – масса электрона; V_n - скорость электрона на n-й стационарной орбите; r_n — радиус этой орбиты; n — целое число: 1, 2, 3, ....

Следуя Бору, рассмотрим атомную систему, состоящую из ядра с зарядом Ze и одного электрона с зарядом - e.

При Z = 1 такая система соответствует атому водорода, при иных Z - водородоподобному атому, т.е. атому с порядковым номером Z, из которого удалены все электроны, кроме одного. Для упрощения расчетов предположим, что электрон вращается по круговой орбите, и масса ядра бесконечно велика по сравнению с массой электрона, а ядро неподвижно.

Центростремительная сила, удерживающая электрон на n-ой стационарной орбите, создается силой кулоновского притяжения к ядру.

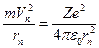отсюда: 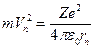, (4)

т.е. при движении электрона по орбите его кинетическая энергия 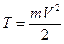и потенциальная энергия 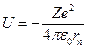связаны отношением 2T = -U (5)

Разделив уравнение (4) на уравнение (3), получим выражение для скорости электрона на n-й стационарной орбите

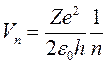. (6)

Полная энергия (Е) электрона на n-й стационарной орбите складывается из кинетической и потенциальной энергий и, с учетом формулы (5), равна:

.

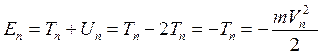Подставляя в эту формулу значение скорости (6), получим для энергий стационарных состояний атома следующее выражение:

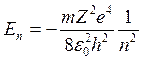
При переходе электрона с орбиты m на орбиту n излучается в соответствии с формулой (3) квант энергии

.

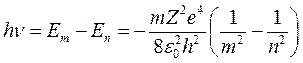Отсюда частота спектральной линии

.

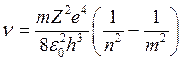В спектроскопии обычно пользуются волновыми числами 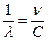. Тогда

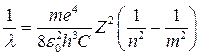(7)

Для водорода (Z = 1) формула (7) принимает вид:

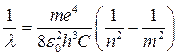(8)

и совпадает с обобщенной формулой Бальмера (1), которая была найдена для волновых чисел спектральных линий атома водорода эмпирическим путем. Из формул (1) и (8) следует, что

R=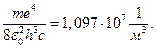

Это значение совпадает с экспериментально определённым значением постоянной Ридберга.

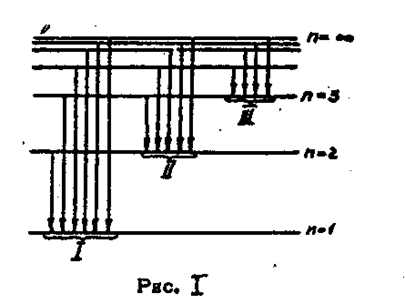
На рис.1 показана схема энергетических уровней и три серии спектральных линий атома водорода.

Переходы с высших уровней на уровень n = 1 соответствуют излучению ультрафиолетовой серии Лаймана (I), для которой из формулы (8) получаем:

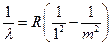, где m = 2, 3, 4, ...

Переходы с высших уровней на уровень n = 2 соответствуют излучению видимой серии Бальмера (II):

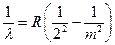, где m = 3, 4, 5, ...

Переходы с высших уровней на уровень n = 3 соответствуют излучению инфракрасной серии Пашена (III):

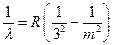, где m = 4, 5, 6, .…

При поглощении света атомом электроны переходят с низших уровней на высшие. При этом атом переходит из основного состояния в возбужденное.

Теории Бора была свойственна внутренняя логическая противоречивость, поэтому она не могла стать последовательной полной теорией атомных явлений. В настоящее время спектры атомов и молекул объясняются в рамках квантовой механики.

Подход к описанию состояния микрочастиц в квантовой механике принципиально отличается от классического. Он не позволяет определить однозначно положение рассматриваемой частицы в пространстве и ее траекторию, как это делается в классической механике, так как в микромире эти понятия теряют смысл, а лишь предсказывает: с какой вероятностью можно обнаружить эту частицу в различных точках пространства. Поэтому квантовая механика имеет статистический характер.

Основу математического аппарата квантовой механики составляет утверждение, что описание состояния системы осуществляется определенной функцией координат и времени Y, характеризующей это состояние. Эту функцию называют волновой. Физический смысл имеет не сама волновая функция, а квадрат ее модуля, который определяет вероятность dw обнаружения объекта (микрочастицы) в элементе объема dV. Если Y-функция нормирована, то dw = |Y|²dV (9)

Выясним свойства волновой функции. В силу сказанного выше о физическом смысле |Y|² волновая функция, Y должна быть:

1. конечной, т.к. вероятность не может быть больше единицы;

2. однозначной;

3. непрерывной, т.к. вероятность не может изменяться скачкообразно.

Таким образом, для описания состояния системы в квантовой механике необходимо знать волновую функцию этой системы. Она находится из уравнения Шредингера, являющегося основным уравнением в нерелятивистской квантовой механике. Уравнение это не выводится, а постулируется, исходя из общих соображений. Справедливость его доказывается совпадением полученных из него теоретических результатов с опытными фактами. В общем случае уравнение Шредингера имеет следующий вид:

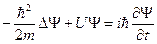(10)

здесь m — масса частицы, U — функция координат и времени, равная взятому с обратным знаком потенциалу силового поля, i — мнимая единица, 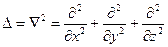- оператор Лапласа, .

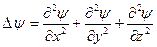Если силовое поле, в котором находится частица, стационарно (не зависит от времени), то потенциал U от времени не зависит и приобретает смысл потенциальной энергии рассматриваемой частицы во внешнем силовом поле. В этом случае Y можно представить в виде произведения двух функций, одна из которых зависит только от координат, а другая только от времени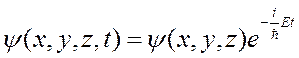

здесь Е — полная энергия частицы, которая в случае стационарного поля с течением времени не меняется.

После подстановки этого выражения в уравнение (10) для функции y(x,y,z) получается следующее уравнение:

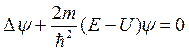, (11)

которое называют уравнением Шредингера для стационарных состояний.

Рассмотрим атом водорода с точки зрения квантовой механики. Подставим в стационарное уравнение Шредингера значение потенциальной энергии электрона в поле ядра:

.

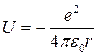Уравнение (11) в этом случае принимает вид:

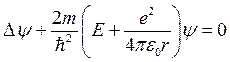(12)

Так как поле ядра атома водорода обладает сферической симметрией, то данное уравнение целесообразно решать в сферической системе координат (r, j, Q). Решение проводят методом разделения переменных, представляя волновую функцию в виде произведения двух функций, одна из которых зависит только от r, а вторая только от угловых координат j , Q.

y(r,Q,j) = R(r)×Y(Q,j)

При таком представлении вероятность частицы иметь значения координаты в интервале от r до r+dr определяется квадратом |rR|².

Решение уравнения Шредингера (12) приводит к следующим основным результатам.

1. Электрон водорода обладает дискретным энергетическим спектром. Собственные значения энергии определяются выражением:

,

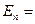
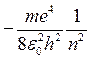где n — главное квантовое число, принимающее любое целое положительное значение (n = 1, 2, 3, ...).

2. Орбитальный момент импульса электрона L может принимать лишь следующий дискретный ряд значений:

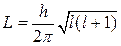
где l — орбитальное (азимутальное) квантовое число. Оно может принимать любое значение из ряда: l = 0, 1, 2, 3, ..., (n-1) — всего n значений. Состояние с l = 0 принято называть s - состоянием, с l = 1 – р - состоянием, c l = 2 – d-состоянием, с l = 3 – f - состоянием и т.д.

3. Орбитальный момент импульса может ориентироваться относительно физически выделенного направления в пространстве (z) лишь таким образом, что проекция его на это направление кратна 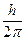, поэтому

,

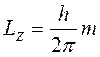m - называется магнитным квантовым числом. Оно может принимать значения:

m =0, ±1, ±2, … , ±l – всего (2 l + 1) значений.

Таким образом, состояние электрона в атоме водорода определяется тремя квантовыми числами - главным n, определяющим энергию состояния E_n; азимутальным l, характеризующим момент импульса электрона L, и магнитным m, определяющим ориентацию L относительно выделенного направления в пространстве. Состояния описываются собственными волновыми функциями Y_n,l,m являющимися решениями уравнения Шредингера (18) .

Уравнение Шредингepa является нерелятивистским. Учет релятивистских эффектов (уравнение Дирака) приводит к существованию у электрона собственного момента количества движения — спина, определяемого квантовым числом s, равным 1/2:

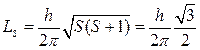
Проекция спина на выделенное направление z может принимать 2s + 1= 2 различных значений: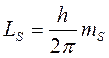

где 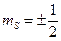— квантовое число проекции спина электрона. С учетом спина состояние электрона в атоме характеризуется четырьмя квантовыми числами: к квантовым числам n, l, m следует добавить спиновое квантовое число m_s.

Отметим, что дискретность физических величин, характерная для явлений атомного мира, в квантовой механике естественным образом вытекает из решения уравнения Шредингера (Дирака), в то время как в теории Бора ее приходилось вводить с помощью дополнительных условий существенно неклассического характера.

Рис. 2

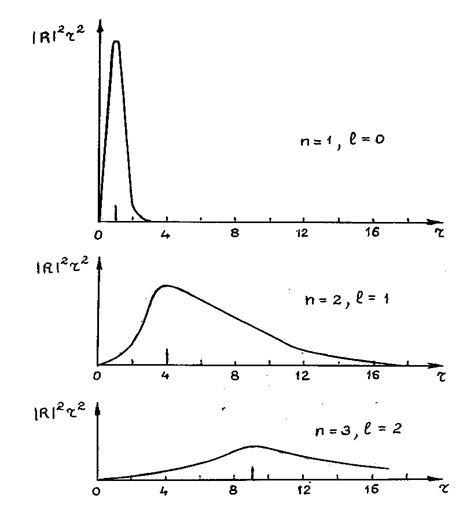
Для иллюстрации пространственного распределения вероятности dw=|y|² на рис.2 приведены графики зависимости функции |R|²r² от r при различных значениях квантовых чисел n, l, m. Функция |R|²r², как уже отмечалось, определяет плотность вероятности нахождения электрона на расстоянии r от ядра. За единицу масштаба для оси r принято значение 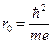, представляющее собой радиус первой круговой орбиты электрона в атоме водорода по теории Бора. Длинными вертикальными черточками на графиках отмечены радиусы соответствующих боровских орбит. Видно, что эти радиусы совпадают с наиболее вероятными расстояниями электрона от ядра.