Краткие теоретические сведения. Метод конечных элементов (МКЭ) – это численный метод решения дифференциальных уравнений с частными производными

Метод конечных элементов (МКЭ) – это численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твердого тела. Суть метода заключается в разбиении области, в которой ищется решение дифференциальных уравнений, на конечное количество элементов.

Элементы имеют общие точки, называемые узлами. Процесс деления модели на малые части называется созданием сетки.

Поведение каждого элемента по всем возможным сценариям опоры и нагрузки хорошо известно. Метод конечных элементов использует элементы различных форм.

Реакция в любой точке элемента интерполируется из реакции узлов элементов. Каждый узел полностью описывается рядом параметров, зависящих от типа анализа и используемого элемента. Для расчетов конструкции реакция узла представляется, в целом, тремя перемещениями и тремя вращениями. Для расчета напряжений решающая программа находит перемещения в каждом узле, а затем вычисляет деформации и конечное напряжение.

Программное обеспечение разрабатывает уравнение, управляющее поведением каждого элемента, учитывая его соединения с другими элементами. Эти уравнения связывают реакцию с известными свойствами материала, ограничениями и нагрузками. В каждом из элементов произвольно выбирается вид аппроксимирующей функции. В простейшем случае это полином первой степени. Вне своего элемента аппроксимирующая функция равна нулю. Значения функций на границах элементов (в узлах) являются решением задачи и заранее неизвестны. Коэффициенты аппроксимирующих функций обычно ищутся из условия равенства значения соседних функций на границах между элементами (в узлах). Затем эти коэффициенты выражаются через значения функций в узлах элементов. Составляется система линейных алгебраических уравнений. Количество уравнений равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы, прямо пропорционально количеству элементов. Далее программа упорядочивает уравнения в большую систему совместных алгебраических уравнений и находит неизвестные.

Когда к телу прикладываются нагрузки, оно пытается компенсировать их воздействие, создавая внутренние силы, которые в целом изменяются от одной точки к другой. Напряжение – это интенсивность этих внутренних сил. Единицы напряжения: сила, деленная на площадь приложения силы.

Эквивалентное напряжение (также называется напряжением von Mises) в отличие от компонентов напряжения не имеет направления, оно представляет собой интегральную величину всех компонентов напряжения, выраженную в ее единицах. Чтобы рассчитать коэффициенты запаса прочности в различных точках, SolidWorks Simulation использует «Критерий текучести von Mises», который точно определяет то, что материал начинает переходить в состояние текучести в какой-то точке, когда эквивалентное напряжение достигает предела текучести материала. Коэффициент запаса прочности в какой-либо точке модели – это отношение предела текучести материала к эквивалентному напряжению в этой точке.

Входные параметря программного комплекса SolidWorks Simulation, реализующего МКЭ, устанавливаются при запуске нового исследования с помощью пунктов меню «Simulation \ Исследование...». После выбора типа исследования, например, «Статический анализ». Затем выбирается пункт меню «Simulation \ Материалы \ Применить материал ко всем...». В появившемся окне выбирается нужный материал из библиотеки материалов и нажимаются кнопки «Применить» и «Закрыть».

Следующие входные параметры устанавливаются пунктами выпадающего меню, запускаемыми с помощью «Simulation \ Нагрузки/крепление» и показанными на рис. 1. С помощью данного меню устанавливаются параметры: крепления модели (пункт «Simulation \ Нагрузки/крепление \ Крепления...»), давления (пункт «Simulation \ Нагрузки/крепление \ Давление...»), приложенных сил (пункт «Simulation \ Нагрузки/крепление \ Сила...»), силы тяжести (пункт «Simulation \ Нагрузки/крепление \ Сила тяжести...»), распределение температуры (пункт «Simulation \ Нагрузки/крепление \ Температура...») и др.

Если на прочность исследуется модель сборки, то с помощью пунктов меню «Simulation \ Контакт/зазоры» задается входной параметр «Набор сопряжений», устанавливающий условия сопряжения (контактов) между компонентами сборки.

Создание сетки МКЭ, которая также является входным параметром, осуществлянтся запуском инструмента «Simulation \ Сетка \ Создать...». Данный инструмент позволяет установить тип и параметры сетки. Создание сетки - это определяющий шаг в анализе конструкции. Программное обеспечение автоматически создает комбинированную сетку для твердого тела, оболочечных и балочных элементов. Сетка на твердом теле соответствует большим или сложным объемным моделям. Элементы оболочки соответствуют тонким деталям (таким, как листовой металл). Балочные элементы соответствуют элементам конструкции.

После созания сетки производится запуск расчета с помощью пункта меню «Simulation \ Выполнить».

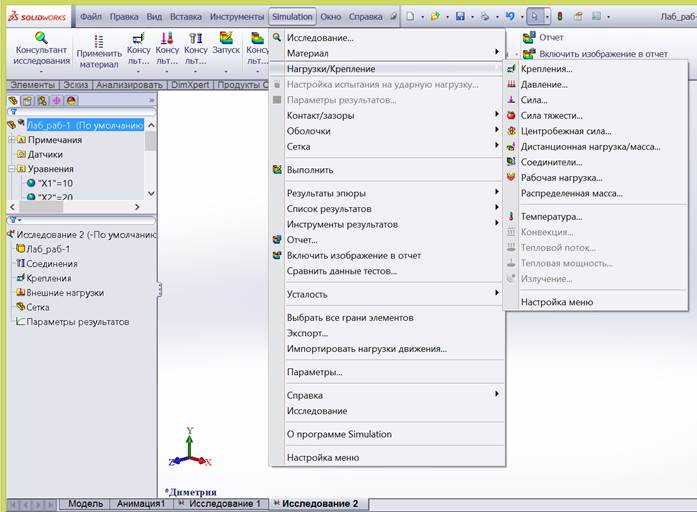
Рис. 1. Задание входных параметров при запуске исследования модели на прочность

Выходные параметры включают в себя результаты расчета, выводимые на экран в виде эпюр напряжений, перемещений и деформаций, а также формируемый отчет в формате Word. Настроить выходные параметры можно после расчета с помощью одного из пунктов меню «Simulation \ Результаты эпюра», например, «Simulation \ Результаты эпюра \ Деформация...». Отчет по результатам расчета формируется после выбора пункта меню «Simulation \ Отчет...».