Теоретическое описание. Средней длиной свободного пробега молекул l называется среднее расстояние, проходимое молекулой между двумя последовательными столкновениями с другими

Средней длиной свободного пробега молекул l называется среднее расстояние, проходимое молекулой между двумя последовательными столкновениями с другими молекулами.

Расстояние d, на которое сближаются при столкновении центры молекул, называется эффективным диаметром молекулы. На рис.2 видно, что чем больше начальная кинетическая энергия молекулы (т.е. чем выше температура), тем меньше d.

Следовательно, эффективный диаметр молекул уменьшается с повышением температуры. Правда, изменение d с ростом температура незначительно. Величина 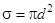называется эффективным сечением молекулы.

Молекулярно-кинетическая теория газов приводит к выводу. Что длина свободного пробега l обратно пропорциональна концентрации n и эффективному поперечному сечению молекулы

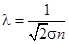. (1)

Эта формула имеет очевидный физический смысл: свободный пробег тем меньше, чем гуще расположены молекулы (т.е. чем больше n) и чем больше перекрываемая каждой молекулой площадь (т.е. чем больше s).

При постоянной температуре плотность молекул n пропорциональна давлению газа. Следовательно, длина свободного пробега обратно пропорциональна давлению:

.

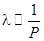Из-за уменьшения эффективного диаметра молекул длина свободного пробега при повышении температуры слабо растет.

Измерить l практически невозможно, но через l выражаются все коэффициенты переноса, которые сравнительно просто можно измерить на опыте.

Динамическая вязкость газов выражается следующим образом: 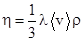(2)

где 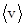– средняя скорость газовых молекул, r – плотность газа.

Сначала нужно измерить вязкость h, затем по формуле (2) вычислить свободный пробег l и, наконец, по формуле (1) вычислить s или d.

Что касается опыта, то нужно выбрать такое физическое явление, чтобы оно позволяло простым образом измерить вязкость воздуха.

В настоящей работе в качестве такого явления используется вязкое течение воздуха через капилляр.

На рис.1 изображена схема установки. Ее основная часть – капилляр L, показанный на рис.3 в увеличенном масштабе.

Если на концах капилляра создать разность давлений 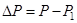, то в капилляре возникает вязкое течение воздуха, профиль скоростей которого показан на рис.3. За время t через него протекает объем воздуха V, который можно вычислить по формуле Пуазейля:

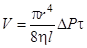(3)

где 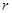– радиус капилляра, 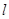– его длина.

Разность давлений на концах капилляра устанавливается благодаря тому, что через кран К из баллона вытекает вода.

Необходимо, чтобы вода вытекала каплями. Тогда давление воздуха в баллоне 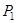и гидростатическое давление столба жидкости высотой h уравновесят атмосферное Р давление т.е.

,

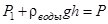откуда следует

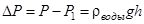
Так как h меняется медленно, причем изменение линейное, то в формулу (3) следует подставлять среднее значение

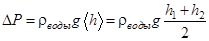(4)

С другой стороны, объем воздуха, прошедшего через капилляр, равен объему вытекающей воды, который легко определяется по формуле

.

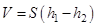Итак, следует измерить 4 величины: V, t, h₁ и h₂. Затем найти 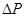по формуле (4) и h из формулы (3).

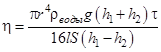(5)

Остается вычислить l, и d. Для этого нужно несколько преобразовать исходные формулы (1) и (2).

Учитывая, что 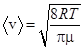и 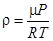, из формулы (2) находим

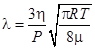(6)

Так как 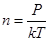, то из формулы (1) имеем:

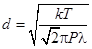(7)

Во всех формулах 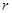– радиус капилляра, 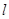– длина капилляра, S – площадь сечения сосуда с водой, 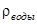=1000 кг/м³ – плотность воды, R = 8,31 Дж/моль×К – универсальная газовая постоянная, k = 1,38×10²³ Дж/К – постоянная Больцмана, m = 0,029 кг/моль – молярная масса воздуха, g = 9,8 м/с² – ускорение свободного падения, T = (t+273)K