Теоретическое описание.
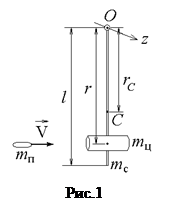 В данной работе физический маятник представляет собой цилиндр массой mц (частично наполненный пластилином), укрепленный на тонком стержне массой mc и длиной l (рис.1). Стержень шарнирно закреплен на горизонтальной оси и может вращаться в вертикальной плоскости вокруг точки О. Положение центра масс цилиндра относительно точки О зададим радиусом-вектором
В данной работе физический маятник представляет собой цилиндр массой mц (частично наполненный пластилином), укрепленный на тонком стержне массой mc и длиной l (рис.1). Стержень шарнирно закреплен на горизонтальной оси и может вращаться в вертикальной плоскости вокруг точки О. Положение центра масс цилиндра относительно точки О зададим радиусом-вектором 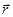 . В маятник стреляют в горизонтальном направлении пулей, имеющей массу mп и скорость
. В маятник стреляют в горизонтальном направлении пулей, имеющей массу mп и скорость 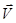 . Пуля входит в пластилин (неупругий удар) и сообщает физическому маятнику угловую скорость
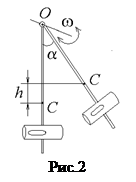
. Пуля входит в пластилин (неупругий удар) и сообщает физическому маятнику угловую скорость  . В результате этого маятник отклонится на угол a и его центр масс С поднимется на высоту h (рис.2).
. В результате этого маятник отклонится на угол a и его центр масс С поднимется на высоту h (рис.2).
Система "пуля-маятник" незамкнутая. Но если считать удар мгновенным, то за время удара маятник не успеет существенно отклониться, и поэтому момент всех внешних сил относительно оси z в течение этого времени будет равен нулю ( 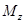 внеш = 0).
внеш = 0).
Отсюда вывод: проекция момента импульса 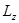 данной системы будет оставаться постоянной относительно оси z (
данной системы будет оставаться постоянной относительно оси z ( 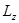 = const). Момент импульса
= const). Момент импульса 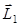 относительно точки О (рис.1) для всей системы перед ударом равен моменту импульса пули:
относительно точки О (рис.1) для всей системы перед ударом равен моменту импульса пули:
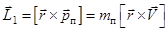 ,
,
где  – импульс пули до удара (маятник находится в покое).
– импульс пули до удара (маятник находится в покое).
Направление вектора 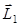 определяется правилом правого винта (см. приложение), а его модуль (и проекция на ось Z)
определяется правилом правого винта (см. приложение), а его модуль (и проекция на ось Z)
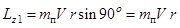 .
.
Так как ось вращения маятника перпендикулярна плоскости его вращения, то момент импульса 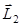 всей системы относительно той же точки О после удара (когда пуля застрянет в пластилине)
всей системы относительно той же точки О после удара (когда пуля застрянет в пластилине)
 .
.
Направление вектора 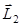 совпадает с направлением вектора
совпадает с направлением вектора 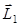 , а модуль (и проекция на ось Z)
, а модуль (и проекция на ось Z)
 .
.
Поскольку система будет вращаться вокруг неподвижной оси Z (см. рис.1), то J – момент инерции всей системы "пуля-маятник" относительно этой оси.
На основании закона сохранения проекции момента импульса на ось z имеем
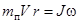 (1)
(1)
Момент инерции J всей системы как величина аддитивная равен сумме моментов инерции составляющих ее тел относительно оси z, т.е.
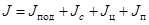 ,
,
где Jпод – момент инерции подшипника (величина его мала по сравнению с Jc, Jц и Jп и ею можно пренебречь);
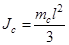 – момент инерции стержня;
– момент инерции стержня;
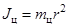 – момент инерции цилиндра (т.к. радиус цилиндра мал по сравнению с r, то момент инерции его рассчитывается, как для материальной точки);
– момент инерции цилиндра (т.к. радиус цилиндра мал по сравнению с r, то момент инерции его рассчитывается, как для материальной точки);
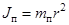 – момент инерции пули.
– момент инерции пули.
Следовательно, в данной работе
 , (2)
, (2)
Из равенства (1) скорость u пули перед ударом в маятник
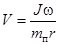 . (3)
. (3)
Угловая скорость w всей системы после удара может быть определена по закону сохранения механической энергии, который в данном случае запишется в виде
 , (4)
, (4)
где 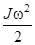 – кинетическая энергия вращательного движения системы после удара пули;
– кинетическая энергия вращательного движения системы после удара пули;
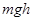 – потенциальная энергия системы после отклонения ее на максимальный угол a.
– потенциальная энергия системы после отклонения ее на максимальный угол a.
Здесь
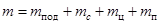 , (5)
, (5)
где m – масса всей системы "пуля-маятник"; mпод – масса подшипника.
Из рис.2 следует, что высота подъема центра масс С системы
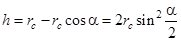 , (6)
, (6)
Выразив w из (4) с учетом (6) и подставив в (3), найдем скорость V пули:
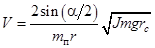 . (7)
. (7)
Центр масс (центр инерции) системы относительно точки О определим по формуле
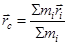 , (8)
, (8)
где 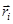 – радиус-вектор центра масс отдельной детали системы;
– радиус-вектор центра масс отдельной детали системы;
mi – масса этой детали.
Из (8) и рис.1 видно, что
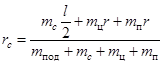 . (9)
. (9)
Приложение
Дата добавления: 2015-03-07; просмотров: 745;
