Теоретическая часть. В данной работе рассматривается кинематика движения тела под углом к горизонту в результате соударения с наклонной плоскостью.
В данной работе рассматривается кинематика движения тела под углом к горизонту в результате соударения с наклонной плоскостью.
|
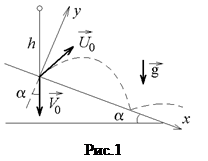
, а отскочив от нее,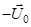 
(см. рис.1). Выберем систему координат, как показано на рис.1, поместив начало координат O в точку первого соударения шарика с наклонной плоскостью. Проекции скоростей и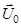 
на ось X равны, то есть Vox = Uox, так как удар можно считать мгновенным, и действие силы тяжести и силы трения за короткое время не окажет существенного влияния на импульс шарика вдоль оси X (закон сохранения проекции импульса). Рассеяние механической энергии при ударе характеризуется коэффициентом восстановления скорости kc.
Коэффициентом восстановления скорости тела при ударе о массивную неподвижную поверхность называется отношение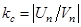 
, где Vn и Un – проекции скоростей тела соответственно до и после удара на нормаль к поверхности.
Для данной работы согласно рис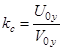.1
(1)
где V0y и U0y - проекции на ось y скоростей шарика соответственно до и после первого удара о наклонную плоскость.
Отскочив от наклонной плоскости в точке O со скоростью 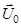, шарик будет двигаться в воздухе с постоянным ускорением 
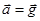(сопротивлением воздуха пренебрегаем) и второй раз ударится о наклонную плоскость. Положение шарика при втором соударении относительно точки O определим из закона движения в проекции на ось x
.
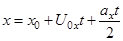При выбранном начале координат и положительном направлении x, как показано на рис.1,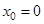 
, 
, 
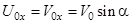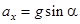, поэтому расстояние x между первым и вторым соударением 
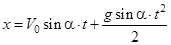(2)
Время t между двумя соударениями найдем из закона движения в проекции на ось y
Здесь y = 0,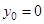 
, с учетом (1) 
, 
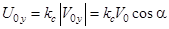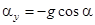. Поэтому
откуда 
(3)
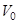определим из закона сохранения полной механической энергии (потерями на сопротивление воздуха пренебрегаем)
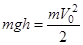(4)
где mgh – потенциальная энергия шарика в точке A, из которой он начинает падать без начальной скорости (в точке О потенциальную энергию шарика принимаем равной нулю); 
– кинетическая энергия шарика в точке О перед ударом о наклонную плоскость.
Из равенства (4) имеем
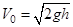(5)
Подставив (3) и (5) в (2), найдем
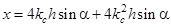
Отсюда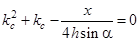 
. Решив это квадратное уравнение, получим
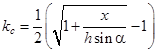(6)
В реальных случаях 0 < kc < 1.
Дата добавления: 2015-03-07; просмотров: 1047;