Электростатика

1. Взаимодействие электрических зарядов в вакууме. Закон Кулона. Электрическое поле и его напряженность. Силовые линии электрического поля.

2. Электрический диполь. Поле диполя.

3. Теорема Остроградского-Гаусса.

4. Работа перемещения заряда в электрическом поле. Потенциал.

5. Медико-биологические применения электростатики.

1. Электростатика изучает взаимодействие и условия равновесия покоящихся электрически заряженных тел, а также свойства этих тел, обусловленные электрическими зарядами.

Взаимодействие электрических зарядов осуществляется в соответствии с законом Кулона, который опытным путем установил, что два точечных заряда взаимодействуют в вакууме с силой F, пропорциональной величинам зарядов q₁ и q₂ обратно пропорциональной квадрату расстояния r между ними и направленной по линии, соединяющей эти заряды.

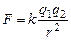(1)

Где k-коэффициент пропорциональности.

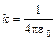, где 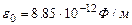-электрическая постоянная. Таким образом

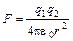(2)

Электрическим полем называется вид материи посредством которого взаимодействуют электрические заряды.

Напряженность электрического поля в данной точке есть вектор, равный по величине силе, действующей, на единичный положительный заряд, помещенный в эту точку и совпадающий с ней по направлению.

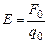(3)

Е измеряется в В/м.

Силовой линией электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля.

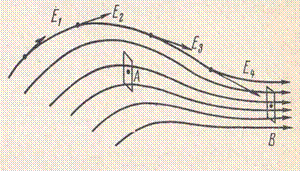
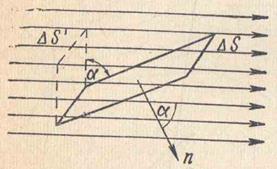
Электрическое поле называется однородным, если во всех его точках напряженность E одинакова.

Напряженность электрического поля точечного заряда определяется формулой.

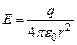(4)

Где r-расстояние от заряда, создающего поле, до точки, в которой определяется напряженность.

Число силовых линий, пронизывающих некоторую поверхность, расположенную в электрическом поле, называется потоком напряженности электрического поля N через эту поверхность

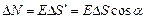(5),

где 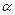- угол между силовой линией и нормалью n к площадке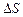

2. Электрический диполь. Поле диполя.

Электрическим диполем называется совокупность двух равных по величине разноименных точечных зарядов q, расположенных на некотором расстоянии друг от друга. Произведение P=ql называется моментом диполя, а l-его плечом. Дипольный момент направлен по оси диполя в сторону положительного заряда.

Напряженность поля на продолжении оси диполя

Напряженность поля вдоль оси диполя равна разности напряженностей Е⁺ и Е^-, создаваемых положительным и отрицательным зарядами.

Е= Е⁺ - Е^-

Если r-расстояние от точки А до середины оси диполя, на основании (4) можно записать

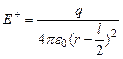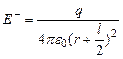и тогда

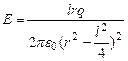
Полагая, что r>>l, пренебрежем 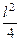. Тогда

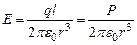(6)

Напряженность поля на перпендикуляре к середине оси диполя.

Напряженность Е в точке А равна Е= Е⁺ + Е^-

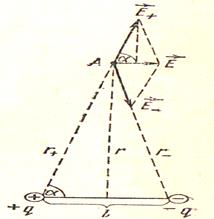
Так как r⁺ =r^- , то Е⁺ = Е^-, тогда Е – диагональ ромба,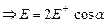

Но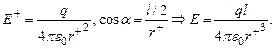

Полагая r>>l, r⁺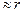

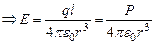(7)

Таким образом, на большом расстоянии от диполя напряженность электрического поля диполя обратно пропорциональна кубу расстояния.

3. Теорема Остроградского-Гаусса.

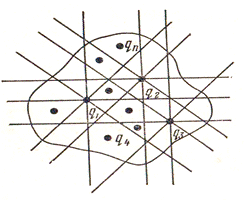
Определим поток напряженности поля электрических зарядов q_1,q_2,…q_n через некоторую замкнутую поверхность, окружающую эти заряды. Поток будем считать отрицательным, если он направлен внутрь поверхности, в противном случае – положительным

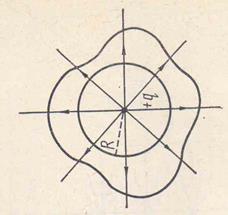
Рассмотрим сначала случай сферической поверхности радиусом R, окружающей один заряд q, находящийся в центре сферы. Согласно (4) напряженность поля на всей сфере одинакова и равна

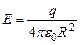(8)

Силовые линии направлены по радиусам, т.е. перпендикулярно поверхности сферы. Это дает возможность применить для расчета потока напряженности N формулу

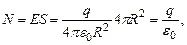(9)

Где 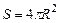- площадь сферической поверхности.

Окружим теперь сферу произвольной замкнутой поверхностью. Каждая силовая линия, пронизывающая сферу, пронижет и эту поверхность. Следовательно, формула (9) справедлива не только для сферы, но и для любой замкнутой поверхности.

В случае произвольной поверхности, окружающей n зарядов, поток напряженности через нее равен сумме потоков, создаваемых каждым из зарядов:

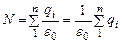
Таким образом, поток напряженности, пронизывающий любую замкнутую поверхность, окружающую электрические заряды, пропорционален алгебраической сумме окруженных зарядов.

Это положение называется теоремой Остроградского-Гаусса.