Однонапрямлені функції та односпрямовані хеш-функції

Діффі та Хеллман запропонували принципово новий спосіб організації секретного зв’язку без попереднього обміну ключами, названий шифруванням з відкритим ключем. При такому способі для зашифровування та розшифровування використовуються різні ключі і знання одного з них не дає практичної можливості визначити другий. Внаслідок цього ключ зашифровування може бути відкритим без втрати стійкості шифру і лише ключ розшифровування має триматися одержувачем у секреті, тому криптосистеми з відкритим ключем називають асиметричними (несиметричними) криптосистемами.

Базовим поняттям криптографії з відкритим ключем є поняття односпрямованої функції (one-way function). За заданим аргументом х Х нескладно обчислити значення цієї функції F(x), тоді як визначити х з F(x) є надто складно, тобто немає алгоритму для розв’язування цього завдання з поліноміальним часом роботи. Теоретично х за відомим значенням F(x) можна знайти завжди, перевіряючи почергово всі можливі значення х доти, поки відповідне значення F(x) не збігатиметься із заданим. Проте практично за значної розмірності множини X такий підхід неможливо здійснити.

Односпрямованою називається функція F(х): X 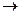Y, х Х, яка має дві властивості:

– існує поліноміальний алгоритм обчислення значень y = F(x);

– не існує поліноміального алгоритму інвертування функції F(x) = y.

Поліноміальним називатимемо алгоритм, виконання якого завершується понад за p(n) кроків, де n – розмір вхідного завдання, який зазвичай вимірюється кількістю символів тексту, що описує це завдання.

Зауважимо, що до сьогодні не доведено існування односпрямованих функцій. Використовування їх за підґрунтя асиметричних алгоритмів шифрування є припустиме лише до того моменту, поки не буде знайдено ефективні алгоритми, які виконували б пошук односпрямованих функцій за поліноміальний час.

Прикладом кандидата на назву односпрямованої функції є модульне піднесення до степеня, тобто функція F(x) = 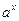mod р, де а – примітивний елемент поля GF(p); р – велике просте число. Те, що ця функція може бути ефективно обчислена навіть за розрядності параметрів у кілька сотень знаків, можна довести на прикладі: 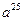можна обчислити за допомогою шести операцій множення (за множення вважається і піднесення до квадрата). Число 25 у двійковій системі обчислення записується як 11001, тобто 25 = .

Тому

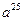(mod р) = ( 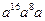) mod р = (((( а) 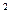) ) 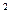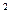а) mod р.

Завдання обчислення функції, оберненої до модульного піднесення до степеня, називають завданням дискретного логарифмування. До сьогодні не відомо жодного ефективного алгоритму обчислення дискретних логарифмів великих чисел.

Односпрямована функція в якості функції зашифровування є непридатна, оскільки, якщо F(x) – зашифроване повідомлення х, то ніхто, враховуючи законного одержувача, не зможе відновити х. Обійти цю проблему можна за допомогою односпрямованої функції з секретом (one-way trapdoor function).

Наприклад, функція 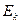: X 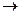Y, яка має обернену функцію 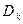: Y 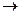X, проте визначити обернену функцію лише за 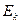без знання секрету k є неможливо.

Односпрямованою функцією з секретом k називають функцію 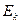: X 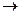Y, залежну від параметра k, яка має такі властивості:

– за кожного k існує поліноміальний алгоритм обчислення значень Ek(x);

– за невідомого k не існує поліноміального алгоритму інвертування Ek;

– за відомого k існує поліноміальний алгоритм інвертування Ek.

Функцію 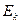можна використовувати для зашифровування інформації, а обернену до неї функцію 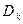– для розшифровування, оскільки за всіх х Х є справедлива рівність

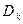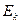( (x)) = x.

При цьому мається на увазі, що той, хто знає, як зашифровувати інформацію, зовсім не обов’язково має знати, як розшифровувати її. Так само як і у випадку з односпрямованою функцією, питання щодо існування односпрямованих функцій з секретом є відкрите.

Для практичної криптографії знайдено кілька функцій – кандидатів на назву односпрямованої функції з секретом. Для них другу властивість не доведено, проте відомо, що завдання інвертування є еквівалентне до розв’язування складної математичної задачі.

Вживання односпрямованої функції з секретом у криптографії дозволяє:

– організовувати обмін шифрованими повідомленнями з використовуванням лише відкритих каналів зв’язку, тобто відмовитися від секретних каналів зв’язку для попереднього обміну ключами;

– включати до завдання розкриття шифру складне математичне завдання і тим самим підвищувати обґрунтованість стійкості шифру;

– розв’язувати нові криптографічні завдання, відмінні від шифрування (електронний цифровий підпис тощо).

Стійкість більшості сучасних асиметричних алгоритмів базується на двох математичних проблемах, які на даному етапі є складнообчислюваними:

– дискретне логарифмування в скінченних полях;

– факторизація великих чисел.

Оскільки сьогодні не існує ефективних алгоритмів розв’язування згаданих проблем, або їхній розв’язок потребує залучення потужних обчислювальних ресурсів, або часових витрат, ці математичні завдання набули широкого використовування в побудові асиметричних алгоритмів.

У всьому різноманітті проблем забезпечення інформаційної безпеки, що розв’язуються за допомогою криптографічних методів та засобів, завдання забезпечення цілісності та вірогідності переданої інформації є на сьогодні одним з найголовніших. З урахуванням сучасних вимог щодо інформаційно- телекомунікаційних систем – це завдання все частіше і частіше перетворюється на серйозну проблему. Надто актуальна вона є у фінансовій сфері, оскільки задля надійного функціонування платіжної системи необхідною умовою є зберігання цілісності та вірогідності усіх документів.

Невід’ємною частиною електронно-цифрового підпису є використовування геш-функцій. Геш-функцією (англ. hash – подрібнювати, змішувати) називається перетворення h, яка перетворює інформаційну послідовність М довільної довжини на послідовність фіксованої довжини h(M), називану геш-кодом. Окрім того, геш-функції широко застосовуються і для розв’язування багатьох інших питань, пов’язаних із забезпеченням захисту потоків даних, наприклад для гешування паролів користувачів з метою подальшого їхнього шифрування та зберігання у базі даних. Цей метод застосовується в ОС Windows NT (використовується геш-функція MD4 разом з DES). Функція гешування може служити за криптографічну контрольну суму – код виявлення змін (MDC – Manipulation Detection Code) або для перевірки цілісності

повідомлення (MIC – Message Integrity Check).

Однією з найважливіших характеристик геш-функцій, що зумовили їхнє широке впровадження у практику, виявилася здатність отримувати з відкритого тексту великої довжини (наприклад в геш-функції SHA максимальна довжина відкритого тексту обмежена 264 бітами) геш-коду набагато меншою довжиною (у російському стандарті ГОСТ Р 34.11–94 довжина геш-коду становить 256 біт, західні геш-функції мають переважно геш-код довжиною 160...180 біт), що в певних випадках дозволяє дуже ефективно скоротити мережний трафік.

Застосовування геш-функцій надає можливість усувати надлишковість відкритого тексту, що при подальшому криптографічному перетворенні геш-коду відкритого тексту позитивно позначається на криптографічних властивостях зашифрованого повідомлення.

До функції h(M) ставляться такі вимоги:

– результат роботи геш-функцій має залежати від усіх двійкових символів

вихідного повідомлення, а також від їхнього взаємного розташування;

– геш-функція має бути стійкою в розумінні звертання;

– геш-функція має бути стійкою в розумінні виявлення колізій.

Область використання геш-функцій:

– захист паролів при їхньому передаванні та зберіганні;

– формування контрольних кодів MDC;

– отримування стисненого зразка повідомлення перед формуванням електронного підпису;

– оперативний контроль перебігу програм.

Існує три методи побудови геш-функцій:

– на базі певної складно обчислюваної математичної задачі;

– на базі алгоритмів блокового шифрування;

– розроблення з нуля.

Кожен із зазначених методів має власні переваги й недоліки, однак, найбільш поширеними сьогодні є останні два. Це пов’язано з тим, що при побудові геш-функцій з нуля, виникає можливість враховувати таку їхню властивість, як ефективна програмна реалізація. Широке застосовування геш- функцій, побудованих на базі алгоритмів блокового шифрування, є наслідком ретельного опрацювання питання стійкості багатьох з існуючих алгоритмів.

Найбільш відомі алгоритми отримування геш-образів повідомлень – MD5, SHA, RIPEMD, ГОСТ Р 34.11–94, TIGER, HAVAL.

MD5 – представник сімейства алгоритмів обчислення геш-функцій MD (Message Digest Algorithm), запропонованого Р. Рівестом [29]; розроблено 1991 р.; перетворює інформаційну послідовність довільної довжини на геш-образ розрядністю 128 біт.

RIPEMD – розроблено в межах європейського проекту RIPE (Race Integrity Primitives Evaluation) Європейського співтовариства; є модифікацією алгоритму MD4; перетворює інформаційну послідовність довільної довжини на геш-образ розрядністю 128 (RIPEMD-128) або 160 біт (RIPEMD-160) [30].

TIGER – розроблено Р. Андерсоном та Е. Біхемом; призначений для реалізації на 64-розрядних комп’ютерах; перетворює інформаційну послідовність довільної довжини на геш-образ розрядністю 192 біти.

HAVAL – односпрямована геш-функція змінної довжини. Функція HAVAL є модифікацією функції MD5. Алгоритм HAVAL опрацьовує повідомлення блоками розміром у 1024 розряди, що є удвічі більше, аніж в алгоритмі MD5. У HAVAL використовується вісім 32-розрядних змінних зчеплення, тобто удвічі більше, аніж в алгоритмі MD5, і змінна кількість раундів опрацювання – від трьох до п’яти (на кожному раунді виконується 16 кроків). Функція HAVAL може видавати геш-значення обсягом у 128, 160, 192, 224 або 256 розрядів.

Розглянемо два приклади практичної реалізації геш-функцій: SHA, побудованої з нуля, і ГОСТ Р 34.11–94 – на базі блочного алгоритму шифрування ГОСТ 28147–89.