Алгоритми Шаміра, RSA та Діффі-Хеллмана
Шифр, запропонований Аді Шаміром (Adi Shamir), дозволяє організовувати обмін секретними повідомленнями відкритою лінією зв’язку для осіб, які не мають захищених каналів та секретних ключів.
Припустімо, два абоненти А та В сполучені лінією зв’язку (рис.). Абонент А хоче передати повідомлення М абонентові В у такий спосіб, щоб ніхто не дізнався про його зміст. Абонент А обирає випадкове велике просте число р і відкрито передає його абонентові В. Потім А обирає два числа – 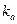 та
та 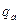 такі, що
такі, що
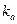
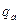 = 1 mod (p – 1).
= 1 mod (p – 1).

Числа 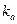 та
та 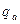 є секретними. Абонент В теж обирає два секретні числа –
є секретними. Абонент В теж обирає два секретні числа – 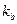 та
та 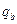 такі, що
такі, що
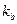
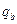
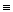 1 mod (p – 1).
1 mod (p – 1).
Після вибору чисел абонент А передає своє повідомлення М, використовуючи триступінчастий протокол. Якщо М < р (М розглядається як число), то повідомлення М передається одразу; якщо М > р, то повідомлення подається у формі М = 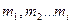 , де усі
, де усі 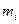 < р, і потім передаються послідовно
< р, і потім передаються послідовно 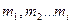 . При цьому для шифрування кожного
. При цьому для шифрування кожного 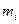 оптимальніше буде обирати випадково нові пари (
оптимальніше буде обирати випадково нові пари ( 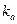 ,
, 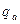 ) та (
) та ( 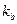 ,
, 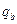 ) – інакше надійність системи знижуватиметься. Сьогодні такий шифр використовується здебільшого для передавання чисел, наприклад секретних ключів, значення яких є менше за р. Тому ми розглядатимемо лише випадок М < р. Подамо опис протоколу.
) – інакше надійність системи знижуватиметься. Сьогодні такий шифр використовується здебільшого для передавання чисел, наприклад секретних ключів, значення яких є менше за р. Тому ми розглядатимемо лише випадок М < р. Подамо опис протоколу.
1) Абонент А обчислює число 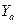
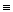
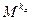 (mod p) і відкритою лінією зв’язку надсилає абонентові В.
(mod p) і відкритою лінією зв’язку надсилає абонентові В.
2) Абонент В, отримавши 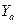 , обчислює число
, обчислює число 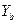
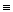
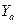
 (mod p) івідкритою лінією зв’язку надсилає абонентові А.
(mod p) івідкритою лінією зв’язку надсилає абонентові А.
3) Сторона А обчислює число С 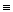
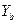
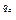 (mod p) й передає його стороні В.
(mod p) й передає його стороні В.
4) Сторона В, отримавши число С, обчислює повідомлення М 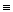 C
C 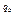 (mod p).
(mod p).
RSA
У довільний спосіб обираються два великі прості числа p та q. Обчислюється добуток n = pq. Обчислюється функція Ейлера: 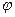 (n) = (p – 1)(q – 1).
(n) = (p – 1)(q – 1).
Довільно обирається просте число e – ключ зашифровування, яке задовольняє умовам e 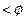 (n); НСД (е,
(n); НСД (е, 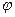 (n)) = 1.
(n)) = 1.
Обчислюється число d – ключ розшифровування, яке є оберненим до числа e, тобто
ed 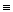 1 (mod
1 (mod 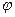 (n)).
(n)).
Пару чисел (e, n) робимо відкритим ключем і розміщуємо у загальнодоступному довіднику, а числа p, q тримаються у секреті, d – секретний ключ. При шифруванні повідомлення М спочатку розкладаємо на цифрові блоки, чиї розміри є менше за n, тобто якщо p та q є 100-розрядними простими числами, то n міститиме близько 200 розрядів і кожен блок повідомлення 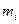 повинен мати близько 200 розрядів у довжину. Зашифроване повідомлення C складатиметься з блоків
повинен мати близько 200 розрядів у довжину. Зашифроване повідомлення C складатиметься з блоків 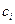 такої самої довжини. Формула зашифровування буде мати вигляд
такої самої довжини. Формула зашифровування буде мати вигляд
C 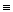 M
M 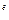 (mod n).
(mod n).
Розшифровування забезпечується операцією піднесення до степеня d за модулем n одержаного шифртексту С:
M 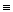 C
C 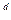 (mod n).
(mod n).
Дата добавления: 2015-03-07; просмотров: 863;
