Законы постоянного тока
Электрическим током называется порядочное движение электрических зарядов. За техническое направление тока принято движение положительных носителей тока. Ток может течь как в проводниках первого рода (металлы), так и в электролитах (проводники второго рода), а также в полупроводниках и газах.
Характеристиками электрического тока являются сила тока I и плотность тока j. Силой тока называется физическая величина численно равная заряду, прошедшему через полное сечение проводника за единицу времени.
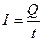 ,
,
где 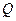 - заряд, прошедший через полное сечение проводника за время t.
- заряд, прошедший через полное сечение проводника за время t.
Плотностью тока называют силу тока через единичное сечение проводника. 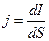 ,
,
где dS – площадь элемента поперечного сечения проводника, dI – сила тока через dS.
Так как рассматриваемый элемент можно выбрать очень маленьким, то плотность тока характеризует электрический ток через рассматриваемую точку поперечного сечения и является его дифференциальной характеристикой в отличии от силы тока, определяющей ток через полное сечение проводника и являющейся, таким образом, интегральной характеристикой. Плотность тока характеризует распределение тока по сечению проводника.
Если носители заряда в проводнике имеют заряд q, концентрация их n , а скорость упорядочного движения при протекании тока V , то заряд, проходящий через единичное сечение проводника в единицу времени будет равен qnV, а это и есть плотность тока. Так как скорость V вектор, то можно ввести вектор плотности тока, определив его следующим образом 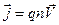 . (1)
. (1)
Очевидно, что он будет перпендикулярен поперечному сечению проводника.
Несколько соединенных между собой проводников образуют электрическую цепь. Если создать в ней электрическое поле, например, разделив заряды так, чтобы на одном конце цепи оказались положительные заряды, а на другом отрицательные, то по цепи потечет электрический ток. Для протекания по электрической цепи постоянного электрического тока необходимо, чтобы она была замкнутой. Однако ток в такой цепи под действием сил только электростатического поля невозможен, так как при движении зарядов силы поля совершают работу по их перемещению, но работа сил электростатического над зарядом при движении его по замкнутому контуру равна нулю. Поэтому для протекания постоянного электрического тока по замкнутой электрической цепи необходимо наличие в ней источника сторонних сил не электростатической природы, который разделял бы заряды во внешнем, по отношению к источнику, участке цепи, создавая в нем тем самым электрическое поле, вызывающее электрический ток.
Характеристикой источника сторонних сил является Электродвижущая сила ε или сокращенно ЭДС. ЭДС источника называется физическая величина, равная работе сторонних сил по перемещению единичного, положительного заряда на данном участке или в замкнутой электрической цепи. 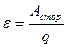 , (2)
, (2)
где 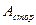 - работа сторонних сил по переносу заряда q на рассматриваемом участке или в замкнутой электрической цепи.
- работа сторонних сил по переносу заряда q на рассматриваемом участке или в замкнутой электрической цепи.
При рассмотрении участка замкнутой электрической цепи, помимо силы тока, вводят понятие падение напряжения. Падением напряжения на участке цепи называется физическая величина, равная работе электростатических и сторонних сил, действующих на данном участке, по переносу единичного, положительного заряда.
Обозначают падение напряжения буквой U.Согласно данному определению U находится по формуле
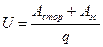 . (3)
. (3)
Здесь 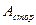 и
и 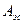 - работы сторонних сил и сил электростатического поля соответственно по переносу заряда q на данном участке.
- работы сторонних сил и сил электростатического поля соответственно по переносу заряда q на данном участке.
Разделим почленно на q правую часть выражения (3) и учтем, что 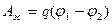 где (
где ( 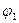 и
и 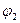 - потенциалы на концах рассматриваемого участка) и в соответствии с (2)
- потенциалы на концах рассматриваемого участка) и в соответствии с (2) 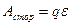 . Тогда для падения напряжения на участке цепи получим следующее выражение
. Тогда для падения напряжения на участке цепи получим следующее выражение 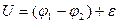 . (4)
. (4)
Если на участке действует несколько сторонних источников, то под ε следует понимать алгебраическую сумму их ЭДС, то есть 
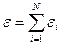 (N – число сторонних источников). ε считается положительной, если при выбранном направлении тока он протекает от минуса к плюсу внутри источника и отрицательной в противном случае.
(N – число сторонних источников). ε считается положительной, если при выбранном направлении тока он протекает от минуса к плюсу внутри источника и отрицательной в противном случае.
Связь между силой тока и падением напряжения на рассматриваемом участке цепи устанавливает закон Ома.
Закон Ома. Сила тока, протекающего по участку цепи, прямо пропорциональна падению напряжения на этом участке.
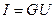 . (5)
. (5)
Коэффициент пропорциональности в формуле закона Ома называется проводимостью данного участка и является его характеристикой. На практике используют обратную проводимости величину R, называемую сопротивлением. 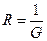 .
.
Формула закона Ома (5) в этом случае примет вид 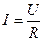 . (6)
. (6)
Сопротивление любого проводника, входящего в состав электрической цепи, зависит от его формы, размеров и свойств материала. Для однородных проволочных проводников электрическое сопротивление можно рассчитать по формуле: 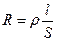 , (7)
, (7)
где: l - длина проводника,
S - площадь его поперечного сечения,
r - удельное электрическое сопротивление, характеризующее электрические свойства материала, из которого изготовлен проводник. В СИ r измеряется в Омах на метр (Ом×м).
Нужно отметить, что сопротивление металлических проводников увеличивается с ростом температуры примерно по линейному закону: 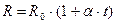 (8)
(8)
Этот рост определяется увеличением удельного сопротивления материала с повышением температуры: 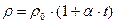
Здесь 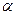 - температурный коэффициент сопротивления (табулирован в таблицах), однако для оценочных расчетов его можно приближенно принять:
- температурный коэффициент сопротивления (табулирован в таблицах), однако для оценочных расчетов его можно приближенно принять: 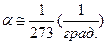 ,
,
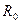 и
и 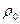 соответственно сопротивление, и удельное сопротивление проводника при 0оС; t - температура по шкале Цельсия.
соответственно сопротивление, и удельное сопротивление проводника при 0оС; t - температура по шкале Цельсия.
Подставляя значение 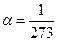 в (8) и учитывая, что абсолютная температура
в (8) и учитывая, что абсолютная температура
Т= t+273 , после несложных преобразований получим 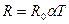 .
.
Из закона Ома вытекает, что при последовательном соединении N элементов электрической цепи полное сопротивление рассматриваемого участка равно сумме сопротивлений всех его элементов, то есть 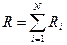 (9)
(9)
При параллельном соединении подобная формула справедлива для проводимостей 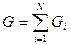 или
или 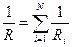 . (10)
. (10)
 |
При рассмотрении электрических цепей различают неоднородные и однородные ее участки. Участок цепи называется неоднородным, если помимо проводников он содержит источники сторонних сил. Закон Ома для такого участка, в соответствии с формулами (4) и (6), имеет вид
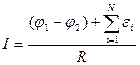 ,
,
где R – полное сопротивление рассматриваемого участка.
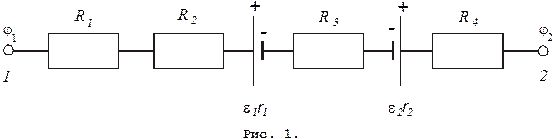
Пример неоднородного участка цепи представлен на рис. 1. Закон Ома для него, если принять, что ток течет от точки 1 к точке 2, запишется в виде
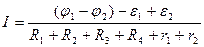 .
.
Здесь r1 и r2 – сопротивления сторонних источников.
Однородным называется участок цепи не содержащий сторонних источников. Для такого участка падение напряжения, в соответствии с формулой (4), равно разности потенциалов на его концах и закон Ома в этом случае примет вид 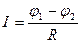 .
.
Если соединить точки 1 и 2 рассматриваемого участка цепи, то получим замкнутую цепь. Так как в этом случае φ1=φ2, то закон Ома, называемый в этом случае законом Ома для замкнутой цепи, запишется в следующей форме: 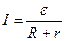 ,
,
где R – полное сопротивление внешней, по отношению к источнику сторонних сил, электрической цепи, а r – внутреннее сопротивление источника.
При протекании электрического тока по проводнику он нагревается, Следовательно, в этом случае совершается работа, которую называют работой тока. Если в проводнике отсутствуют сторонние силы, то работа тока представляет собой работу сил электростатического поля, существующего в проводнике, которая совершается при движении в нем электрических зарядов. В отсутствии механических перемещений проводника и химических реакций в цепи эта работа целиком идет на нагревание проводника, Выделяющееся при этом количество теплоты определяется законом Джоуля-Ленца.
Закон Джоуля-Ленца. Количество теплоты Q, выделяющееся в проводнике при протекании по этому проводнику электрического тока, равно произведению квадрата силы тока на сопротивление проводника и на время протекания электрического тока.
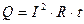 . (11)
. (11)
Мощность тока Р - это работа, совершаемая в единицу времени. Так как в нашем случае dA = dQ , то для мощности получим с учетом формулы (11)
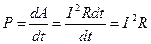 (12)
(12)
В замкнутой электрической цепи полезная мощность выделяется на сопротивлении нагрузки во внешней цепи. Согласно ( 12 ) она равна: Pн =I2Rн
Полная или затраченная мощность Рз выделяется во всей электрической цепи Рз=I2R,
где R=Rн+r – полное сопротивление электрической цепи, равное сумме сопротивления нагрузки Rн и внутреннего сопротивления r источника тока. (Предполагается, что сопротивлением подводящих проводов можно пренебречь).
Отношение полезной мощности к затраченной называют коэффициент полезного действия 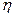 источника тока
источника тока 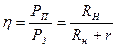 (13)
(13)
При изменении 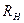 и постоянном
и постоянном 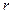 изменяется полезная мощность и коэффициент полезного действия.
изменяется полезная мощность и коэффициент полезного действия.
При 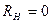
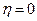 , с ростом RН , КПД увеличивается, асимптотически приближаясь к единице при
, с ростом RН , КПД увеличивается, асимптотически приближаясь к единице при 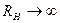 (разомкнутая цепь). Однако, практически разомкнутый элемент никакой полезной мощности не выделяет, поскольку при этом отсутствует электрический ток.
(разомкнутая цепь). Однако, практически разомкнутый элемент никакой полезной мощности не выделяет, поскольку при этом отсутствует электрический ток.
Определим, в каком случае на нагрузке выделяется максимальная мощность. Для этого исследуем 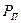 на максимум:
на максимум:
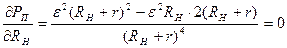 ,
, 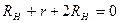 и
и 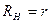
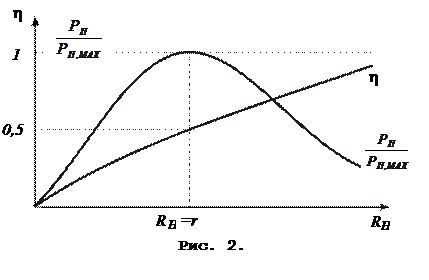 Проведенный расчет показывает, что максимум полезной мощности получается, когда сопротивление нагрузки равно внутреннему сопротивлению источника тока. Так как, согласно закону Ома для замкнутой цепи
Проведенный расчет показывает, что максимум полезной мощности получается, когда сопротивление нагрузки равно внутреннему сопротивлению источника тока. Так как, согласно закону Ома для замкнутой цепи
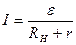 , то
, то
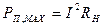 =
= 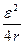
Графики зависимости 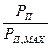 и КПД от
и КПД от 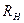 приведены на рис. 2
приведены на рис. 2
Законы Ома и Джоуля - Ленца в дифференциальной форме.
Выделим в проводнике элементарный объем, ограниченный линиями тока, длиной 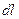 и сечением
и сечением 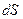 с удельным сопротивлением
с удельным сопротивлением  (Рис. 3).
(Рис. 3).
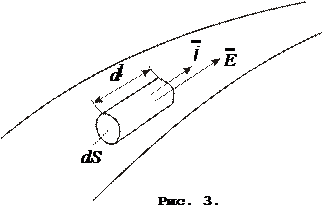 Выбранный элемент представляет собой однородный участок, поэтому падение напряжения U на нем, будет равняться разности потенциалов
Выбранный элемент представляет собой однородный участок, поэтому падение напряжения U на нем, будет равняться разности потенциалов 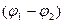 на концах элемента. В однородном электрическом поле
на концах элемента. В однородном электрическом поле
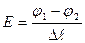 или
или 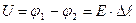
Сила тока dI через рассматриваемый элемент равна 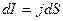 ( где j – плотность тока), а сопротивление
( где j – плотность тока), а сопротивление 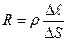 .Подставляя эти выражения в закон Ома для участка цепи получим:
.Подставляя эти выражения в закон Ома для участка цепи получим: 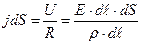 или
или 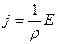
Так как векторы 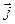 и
и 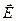 в данном случае параллельны, то последнюю формулу можно записать в векторном виде:
в данном случае параллельны, то последнюю формулу можно записать в векторном виде: 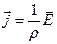 или
или 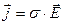 (14)
(14)
где 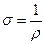 - удельная электрическая проводимость.
- удельная электрическая проводимость.
Применим закон Джоуля – Ленца к этому же элементарному объему. Подставляя в формулу (13) выражение для силы тока через его плотность и сопротивление рассматриваемого объема, получим:
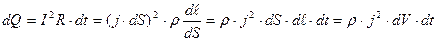 (15)
(15)
Здесь учтено, что 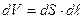 - объем выделенного элемента в проводнике.
- объем выделенного элемента в проводнике.
Введем новую физическую величину, называемую удельной тепловой мощностью. По определению это количество теплоты, выделяющееся в единице объема проводника за единицу времени при протекании по проводнику электрического тока:
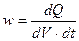
Отсюда dQ=wdVdt. Подставив это количество теплоты в уравнение (15) получим:
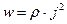 (16)
(16)
Выражения (14) и (16) называют законом Ома и законом Джоуля – Ленца в дифференциальной форме соответственно, так как в силу малости выделенного элементарного объема они относятся не ко всему проводнику, а к рассматриваемому элементу проводника. Уравнения же (6) и (11) называют законом Ома и законом Джоуля – Ленца в интегральной форме.
Формулу (16) можно представить в другом виде, если использовать закон Ома в дифференциальной форме. Подставляя в нее значение j из формулы (14), после несложных преобразований получим 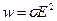 . (17)
. (17)
Класссическая электронная теория электропроводности металлов
Металлы отличаются от диэлектриков и полупроводников значительно большей электропроводностью. Классическая теория электропроводности металлов была разработана Друде и уточнена Лоренцем. При теоретическом рассмотрении протекания электрического тока по металлическому проводнику Друде сделал следующие предположения:
1. Носителями электрического тока в металле являются свободные электроны, утратившие связь со своими атомами. Экспериментально это было доказано опытами Рикке, Стюарта и Толмена.
2. Электронный газ в металлическом проводнике по своим свойствам идентичен идеальному газу.
3. При движении электроны сталкиваются не между собой, а с ионами кристаллической решетки полностью отдавая им при этом кинетическую энергию упорядоченного движения.
Согласно этим предположениям, в отсутствие электрического поля, свободные электроны движутся хаотически. Средняя арифметическая скорость такого движения электронов в соответствие с гипотезой Больцмана для идеального газа равна: 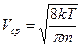 ,
,
при расчете Vср оказывается по порядку величины равной 105 м/с.
При создании электрического поля в проводнике на хаотическое движение электронов накладывается упорядоченное движение, определяемое воздействием поля на свободные электроны металла. Скорость движения электронов в этом случае равна сумме двух скоростей – скорости теплового хаотического движения 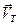 , по модулю равной Vср., и скорости упорядоченного движения
, по модулю равной Vср., и скорости упорядоченного движения 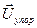
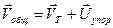
Скорость упорядоченного направленного движения 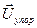 может быть определена по порядку величины из экспериментально полученного предельного значения плотности тока для медного проводника jмеди=10 А/мм2. Если подставить это значение в формулу
может быть определена по порядку величины из экспериментально полученного предельного значения плотности тока для медного проводника jмеди=10 А/мм2. Если подставить это значение в формулу 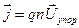 , то среднее значение Uупор окажется порядка 10-3 м/с.
, то среднее значение Uупор окажется порядка 10-3 м/с.
В теории Друде полагалось, что скорость теплового хаотического движения одинакова у всех электронов. Лоренц учел распределение электронов по скоростям, однако это существенно не сказалось на результатах, полученных Друде. Поэтому, ввиду большей простоты и наглядности, используем подход Друде.
Возникновение электрического тока в проводнике связано с появлением у электронов скорости Uупор, возникающей под действием электрического поля. Согласно третьему положению эта скорость изменяется от нулевого значения сразу после столкновения с ионом до некоторого максимального перед следующим столкновением. Затем все это повторяется. Таким образом, в промежутке между двумя последовательными столкновениями электрона с ионами движение его равноускоренное под действием сил электрического поля, без начальной скорости. График такого движения представлен на рис. 4. τ на этом графике - время свободного пробега электрона.
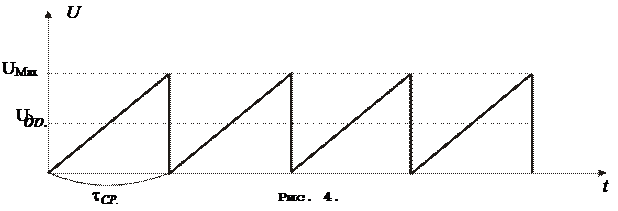
Временем свободного пробега называют среднее время движения электрона между двумя последовательными столкновениями с ионами. Так как для модулей VТ и Uупор справедливо соотношение 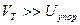 , то время свободного пробега электрона будет определяться только скоростью VT, так как
, то время свободного пробега электрона будет определяться только скоростью VT, так как 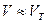 . Поэтому
. Поэтому 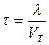 , где l - длина свободного пробега электрона.
, где l - длина свободного пробега электрона.
Длина свободного пробега электрона это среднее расстояние, проходимое электроном между двумя его последовательными столкновениями с ионами. Оно примерно равно постоянной решетки.
Согласно графику скорости, представленному на рис. 4, упорядоченное движение происходит с некоторой средней скоростью 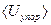 , которую называют скоростью дрейфа Uд. В соответствии с графиком она равна средней скорости направленного движения за время τ. По определению средней скорости
, которую называют скоростью дрейфа Uд. В соответствии с графиком она равна средней скорости направленного движения за время τ. По определению средней скорости
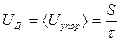 , (18)
, (18)
где S- путь, пройденный электроном за время τ.
Так как движение электронов в это промежуток времени равноускоренное без начальной скорости, то 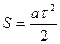 .
.
Значение ускорения 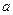 найдем из уравнения динамики движения электрона
найдем из уравнения динамики движения электрона 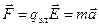 ,
,
где qэл = е – заряд электрона, 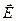 - напряженность электрического поля, m – масса электрона,
- напряженность электрического поля, m – масса электрона, 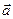 -его ускорение. Векторы
-его ускорение. Векторы 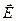 и
и 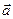 сонаправлены, следовательно, справедливо и скалярное равенство:
сонаправлены, следовательно, справедливо и скалярное равенство:
еЕ = mа. Отсюда 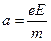 (19)
(19)
и для S получим 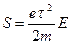 . Тогда, согласно (18),
. Тогда, согласно (18), 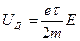 . (20)
. (20)
Так как коэффициент пропорциональности между скоростью упорядоченного движения носителей зарядов и напряженностью электрического поля называют подвижностью b носителя, то в соответствие с формулой (20), подвижность свободного электрона в металле будет равна: 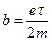 .
.
Для нахождения плотности тока, созданного упорядоченным движением электронов в металле, используем формулу (1): j=enUД ,
где е заряд электрона и n – концентрация свободных электронов в металле. Подставляя сюда найденные значения UД из (20) получим: 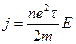
Сравнивая с (14) видим, что мы получили выражение для закона Ома в дифференциальной форме, причем удельная электропроводность будет равна:
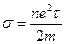 или, с учетом
или, с учетом 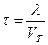 , получим:
, получим: 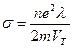 . (21)
. (21)
Рассмотрим теперь тепловое действие тока. Нагревание проводника связано с тем, что при столкновении электрона с ионом, последнему передается кинетическая энергия упорядоченного движения электрона. В результате энергия теплового движения ионов возрастает, что эквивалентно нагреванию проводника. Найдем энергию, передаваемую электронами ионам кристаллической решетки в единице объема проводника за единицу времени. Другими словами найдем удельную тепловую мощность w. Она равна произведению числа столкновений, испытываемых всеми электронами с ионами единицы объема за единицу времени, на кинетическую энергию WК Max упорядоченного движения электрона, которую он имеет непосредственно перед соударением w=NстWК .Max . (22)
Число столкновений Nст найдем, умножив концентрацию электронов n на число столкновений nст одного электрона с ионами за единицу времени. Определить nст можно разделив единицу времени (1 секунду) на время свободного пробега электрона в кристаллической решетке металла 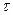 , то есть.
, то есть. 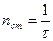
Тогда 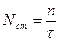 . Подставляя это значение в формулу (22) получаем:
. Подставляя это значение в формулу (22) получаем: 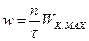 (23)
(23)
В этой формуле 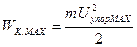 ,
,
где Uупор,MAX – максимальное значение скорости упорядоченного движения, которую имеет электрон перед столкновением с ионом. Так как движение электрона равноускоренное без начальной скорости, то Uупор,MAX=at и, в соответствие с формулой (19) равна: 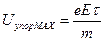 . Тогда
. Тогда 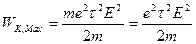 и подставляя это выражение в формулу (23) для удельной тепловой мощности получаем:
и подставляя это выражение в формулу (23) для удельной тепловой мощности получаем:
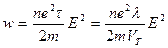 . (24)
. (24)
С учетом формулы (21) это выражение можно представить в виде 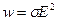 .
.
Сравнивая с (21) видим, что мы получили закон Джоуля-Ленца в дифференциальной форме.
Дата добавления: 2015-03-07; просмотров: 1804;
