Методика проведения эксперимента

В данной лабораторной работе необходимо экспериментальным путем получить зависимость энергетической светимости R от абсолютной температуры Т. Однако прямое измерение энергетической светимости (1.1) является весьма нетривиальной технической задачей. В результате установившегося теплового равновесия вся подводимая к излучателю энергия целиком преобразуется в энергию теплового излучения, т.е. Р = Ф. Мощность электрического тока P = IU равна энергии теплового излучения. Это равенство носит всего лишь приближенный характер, так как часть подведенной энергии передается в виде тепла от излучателя в окружающую среду.

Порядок выполнения работы

1. Включить ЛАТР в сеть, предварительно установив ручку его регулировки в нулевое положение. Включить установку.

2. Вращая ручку регулировки ЛАТРа, подать напряжение на лабораторную установку. При этом не допускать зашкаливания стрелок измерительных приборов.

3. После установления стационарного режима (стрелки приборов неподвижны) измерить по приборам значения напряжения, тока и ТЭДС термопары.

4. Последовательно увеличивая напряжение, подаваемое на нить, выполнить измерения 6–8 раз. Для уменьшения погрешностей не рекомендуется проводить измерения в области температур, близких к комнатной температуре. Данные занести в табл. 1.1.

5. Произвести вычисления для построения графика

Таблица 1.1

№	U, B	I, A	I × U/S, A × B/м2		ln	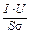ТЭДС, мВ	Т, К	ln T
…

Методика измерений и обработка результатов

Измерение потока энергии излучения Ф платиновой нити заменяется измерением подводимой к ней электрической мощности Р = I × U, где I – сила тока, а U – падение напряжения в цепи накала нити. Площадь (цилиндрической поверхности нити 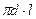, где d = 0,2 мм – диаметр, а l = 7 7 см – длина платиновой нити. Таким образом, в соответствии с выражением (1.1), величина энергетической светимости нагретого тела в данной работе рассчитывается по формуле: R = I × U/S.

Чтобы определить температуру платиновой нити, необходимо располагать градуировочным графиком термопары (зависимость температуры от ТЭДС). В хорошем приближении в данной работе можно считать, что зависимость ТЭДС используемой термопары от абсолютной температуры Т носит линейный характер:

ТЭДС = k × (T – T_ср), (1.6)

где Т_ср – абсолютная температура окружающей среды, а коэффициент пропорциональности k = 0,074 мВ/⁰К (для данной температуры). С помощью формулы (1.6) в настоящей работе рассчитывается абсолютная температура нити Т по измеренным значениям ТЭДС термопары.

После того, как экспериментальным путем получена зависимость энергетической светимости R от абсолютной температуры Т, необходимо найти неизвестные α и z графическим путем. Для этого нужно:

1) Построить график зависимости энергетической светимости 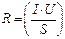от Т.

2) Определить коэффициент серости a платиновой нити и показатель степени температуры z. С этой целью прологарифмируем обе части выражения (1.5), предварительно разделив обе части на s. Получим:

ln T. (1.7)

график выражения (1.7) представляет линейную функцию вида:

y = в + кx.

В данной работе нас интересует второй член в (1.7), где z=k – угловой коэффициент.

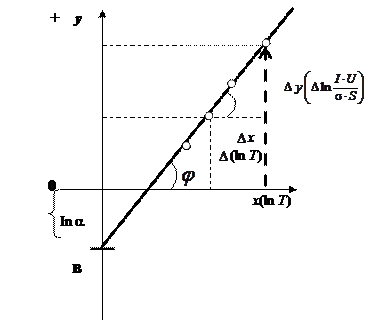
Рис. 1.2

График зависимости энергетической светимости от температуры нагретого тела в координатах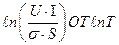

По экспериментальным точкам провести прямую. Находим z по тангенсу угла наклона прямой tg j = z, z .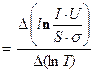

Порядок нахождения α – коэффициент серости. Выразим из (1.7) размерность

[R]=[α][ 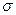]۬·[T^z]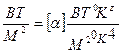

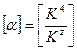
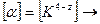
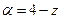
Контрольные вопросы

1. Какова особенность теплового излучения?

2. Назовите основные характеристики теплового излучения.

3. Сформулируйте основные законы теплового излучения.

4. Определите понятие абсолютно черного тела, серого тела, коэффициента серости.

5. Как объяснила теория М. Планка экспериментальные законы теплового излучения абсолютно черного тела?

6. Как провести расчет искомых величин a и z.

7. Зная величины a и z провести анализ, как излучение, данное нагретого тела отличается от излучения абсолютно черного тела.

8. Вывод. Проанализируйте полученные результаты.

Список литературы

1. Детлаф, А.А. Курс физики / А.А. Детлаф, Б.М. Яворский. – М.: Высшая школа, 1989. – 607 с. Т.3.

2. Ландсберг, Г.С. Оптика / Г.С. Ландсберг. – М.: Наука, 1976. – 926 с.

3. Иродов, И.Е. Квантовая физика. Основные законы: Учеб. пособие для вузов / И.Е. Иродов. – М.: Лаборатория базовых знаний, 2001. – 27 с.

4. Савельев, И.В. Курс физики. Т. 3. Квантовая оптика / И.В. Савельев. – М.: Наука, 1989. – 301 с.