Регрессионный анализ

Регрессионный анализ производится при помощи модуля «Statistics/Multiple Regressions».

В диалоговом окне этого модуля (рис.5.28.) при помощи кнопки «Variables» указываются зависимые (dependent) и независимые (independent) переменные.

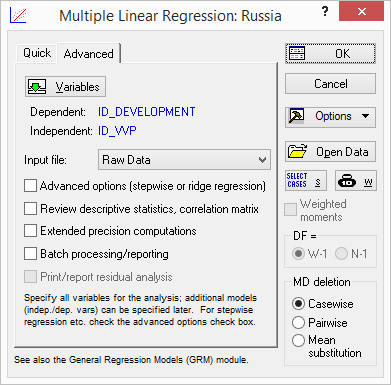
Рисунок 5.29. Диалоговое окно модуля «Multiple Regressions»

В настройках регрессионного анализа указывается:

1. Advanced options (stepwise or ridge regression) – пошаговая или гребневая регрессия.

2. Review descriptive statistics, correlation matrix – описательные статистики, матрицы корреляций.

3. Extended precision computation – вычисления с повышенной точностью.

4. Batch processing/reporting – пакетная обработка/печать.

5. Print/report residual analysis – печать результатов анализа остатков.

Множественную регрессию можно проводить пошагово. В этом случае в модель будут пошагово включаться (или исключаться) переменные, которые вносят наибольший (наименьший) вклад в регрессию на данном шаге.

Определим зависимость индекса реального валового внутреннего продукта (ВВП) на душу населения от индекс общественного развития. После того, как все опции диалогового окна регрессионного анализа выставлены, нажатие на кнопку «ОК» приведет к появлению окна представленного на рис.5.29, где в поле «Method» необходимо выбрать «Forward stepwise».

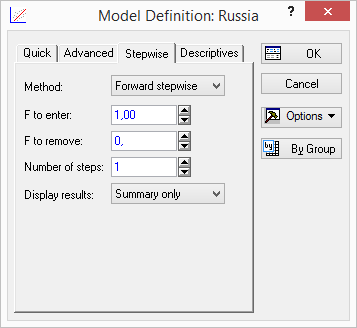
Рисунок 5.30. Выбор метода пошаговой регрессии

По нажатию кнопки «OK» отобразятся результаты регрессионного анализа (рис.5.30).

Рисунок 5.31. Окно просмотра результатов регрессионного анализа

В верхней части окна приводятся наиболее важные параметры полученной регрессионной модели:

1. Multiple R - коэффициент множественной корреляции. Характеризует тесноту линейной связи между зависимой и всеми независимыми переменными. Может принимать значения от 0 до 1.

2. R2 или RI - коэффициент детерминации. Численно выражает долю вариации зависимой переменной, объясненную с помощью регрессионного уравнения. Чем больше R², тем большую долю вариации объясняют переменные, включенные в модель.

3. adjusted R - скорректированный коэффициент множественной корреляции. Этот коэффициент лишен недостатков коэффициента множественной корреляции. Включение новой переменной в регрессионное уравнение увеличивает RI не всегда, а только в том случае, когда частный F-критерий при проверке гипотезы о значимости включаемой переменной больше или равен 1. В противном случае включение новой переменной уменьшает значение RI и adjusted R² .

4. adjusted R2 или adjusted RI - скорректированный коэффициент детерминации. Скорректированный R² можно с большим успехом (по сравнению с R²) применять для выбора наилучшего подмножества независимых переменных в регрессионном уравнении

5. F - F-критерий.

6. df - число степеней свободы для F-критерия.

7. p - вероятность нулевой гипотезы для F-критерия.

8. Standard error of estimate - стандартная ошибка оценки (уравнения).

9. Intercept - свободный член уравнения.

10. Std.Error - стандартная ошибка свободного члена уравнения.

11. t - t-критерий для свободного члена уравнения.

12. p - вероятность нулевой гипотезы для свободного члена уравнения.

13. Beta - b-коэффициенты уравнения.

Это стандартизированные регрессионные коэффициенты, рассчитанные по стандартизированным значениям переменных. По их величине можно сравнить и оценить значимость зависимых переменных, так как b-коэффициент показывает на сколько единиц стандартного отклонения изменится зависимая переменная при изменении на одно стандартное отклонение независимой переменной при условии постоянства остальных независимых переменных.

При помощи кнопок диалогового окна «Multiple Regressions Results» результаты регрессионного анализа можно просмотреть более детально.

Кнопка «Summary: Regression results» - позволяет просмотреть основные результаты регрессионного анализа (рис.5.31): BETA - b-коэффициенты уравнения; St. Err. of BETA - стандартные ошибки b-коэффициентов; В - коэффициенты уравнения регрессии; St. Err. of B - стандартные ошибки коэффициентов уравнения регрессии; t (95) - t-критерии для коэффициентов уравнения регрессии; р-level- вероятность нулевой гипотезы для коэффициентов уравнения регрессии.

Рисунок 5.32. Итоговая таблица регрессии

Таким образом, уравнение регрессии имеет вид:

ID_DEVELOPMENT = 0,269906*ID_VVP + 0,618848.

Важным элементом анализа является оценка адекватности модели. После того как доказана адекватность модели, полученные результаты можно уверенно использовать для дальнейших действий. Анализ адекватности основывается на анализе остатков. Остатки представляют собой разности между наблюдаемыми значениями и модельными, то есть значениями, подсчитанными по модели с оцененными параметрами.

После нажатия на кнопку «ОК» в окне «Multiple Regression Result» (рис.5.30) на экране появиться диалоговое окно «Residual Analysis» (Анализ остатков) (рис.5.32).

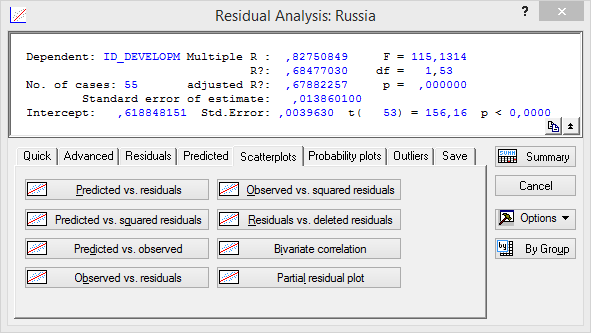
Рисунок 5.33. Диалоговое окно «Residual Analysis»

В этом окне на вкладке «Scatterplots» (Разбросы) по кнопке «Predicted vs. residuals» (Предсказательные относительно остатков) можно посмотреть график (рис.5.33), который говорить о достаточной адекватности модели.

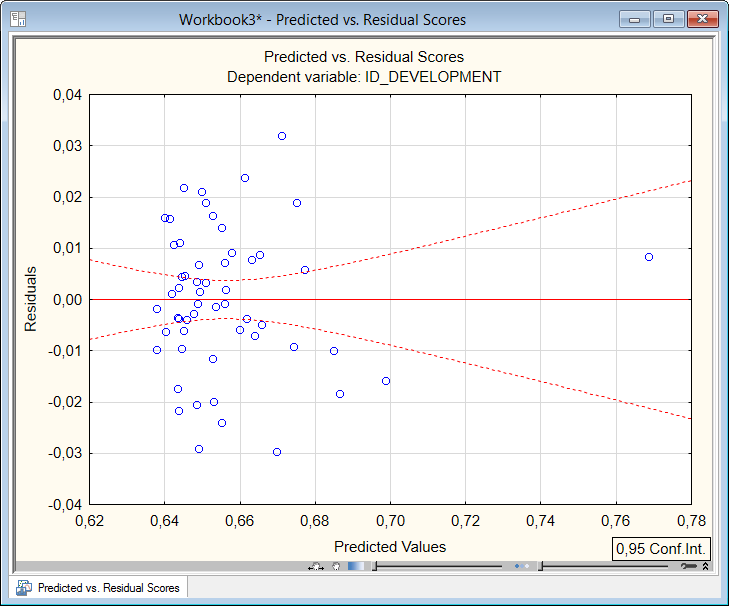
Рисунок 5.34. График остатков

Примечание

Часто, если остатки не являются нормальными, а также для стабилизации дисперсии применяют преобразования зависимых и независимых переменных, например, извлечение квадратного корня или логарифмическое преобразование зависимых переменных.

В окне, представленном на рис.5.32 на вкладке «Scatterplots» (Разбросы) по кнопке «Bivariate correlation» (Двумерная корреляция) можно посмотреть графически результат множественной регрессии. Для начала необходимо выбрать переменные для осей, как это сделано на рис.5.34.

Рисунок 5.35. Окно выбора осей для построения корреляционного поля

По нажатию на кнопку «ОК» в окне, представленном на рис.5.34, на экране появится корреляционное поле, где по оси X расположены значения остатков переменной ID_VVP, а по оси Y – переменнойID_DEVELOPMENT. Так же на этом графике записано уравнение регрессии для построенной модели и коэффициент корреляции.

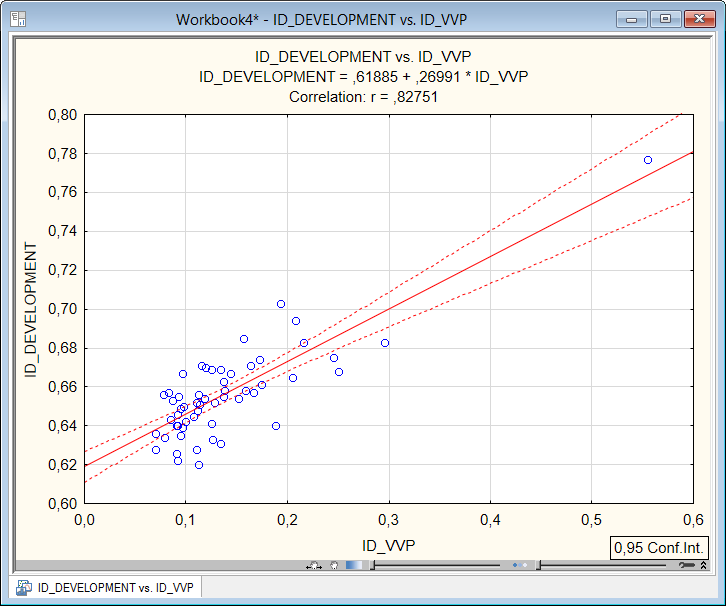
Рисунок 5.36. Корреляционное поле для переменных ID_VVP и ID_DEVELOPMENT