Определение модуля сдвига с помощью пружинного маятника.

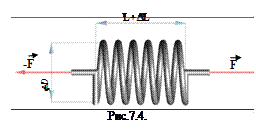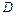Рассмотрим кручение при деформации цилиндрической пружины. На рис.7.4 цилиндрическая пружина диаметром и длиной 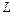, подверженная растяжению до длины 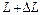двумя равными и противоположно направленными вдоль ее оси силами . Будем рассматривать пружину, как винтовую линию с пренебрежимо малым шагом, таким, что каждый ее виток перпендикулярен силам, действующим на пружину. Момент сил, действующий в любом сечении витка пружины в таком случае является постоянной величиной, равной 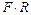, где 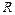- радиус пружины. Вектор момента сил направлен по касательной к витку, и следовательно, вызывает деформацию чистого кручения витков пружины. Следствием этой деформации будет изменение длины пружины, т.е. ее линейная деформация.

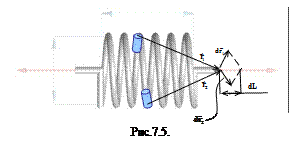Проследим геометрическую связь деформации кручения бесконечно малого элемента витка пружины 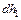и удлинения пружины 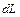. Рассмотрим бесконечно малый вектор перемещения 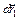точки приложения силы 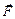, находящейся на оси пружины (см. рис. 7.5). Этот вектор направлен перпендикулярно вектору 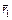, соединяющему элемент витка с точкой приложения силы. Величина его равна 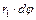, где 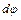- угол кручения элемента витка. Направление вектора перемещения образует с осью пружины угол 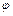. На рис. 7.5 изображен также вектор перемещения 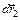точки приложения силы при кручении элемента витка, расположенного на одном диаметре с первым элементом и имеющим такую же длину. По этой причине модули обоих векторов перемещений одинаковы и мы обозначим их через 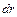. Видно, что сумма этих векторов направлена по оси пружины и ее величина равна 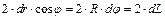. Таким образом, перемещение точки приложения силы при кручении одного элемента витка на угол 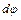выражается формулой 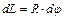. Угол кручения вычислим с помощью соотношения 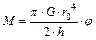, где 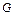- модуль сдвига; 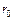- диаметр проволоки пружины; 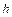- длина пружины; тогда: 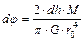. Полную линейную деформацию 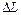пружины с общей длиной всех 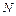витков 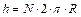можно получить с помощью интегрирования:

где: d – диаметр проволоки пружины, D – диаметр пружины, N - количество витков. Следовательно, жесткость пружины:

. (7.13)

Из формулы (7.13) вытекает связь модуля сдвига и жесткостью пружины:

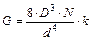(7.14)

Для экспериментального определения жесткости пружины в данной работе изучаются свободные колебания груза известной массы 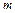, подвешенного на пружине (пружинный маятник). Зависимость отклонения от равновесного положения груза от времени 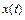подчиняется следующему уравнению динамики: 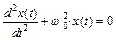. Решение этого уравнения, как следует из теории, имеет вид: 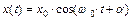, где амплитуда 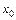и начальная фаза 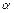определяются начальными условиями; 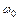– угловая частота крутильных колебаний, период которых Т равен: 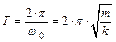, откуда . Подставляя этот результат в формулу (7.14), получаем следующую расчетную формулу:

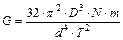. (7.15)