Определение модуля Юнга методом изгиба.

Одним из методов определения модуля Юнга является метод изгиба стержня прямоугольной формы длиной 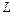, положенного обоими концами на опорные стальные призмы ВВ и нагруженного в середине внешней силой 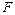(рис. 7.2). При такой деформации верхние слои стержня сжимаются, нижние растягиваются, а средний слой, называемый нейтральным, сохраняет свою длину и претерпевает искривление. Перемещение 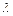, которое получает нейтральный слой стержня, называется стрелой прогиба. Зная стрелу прогиба, можно определить модуль Юнга. Рассмотрим элемент длины стержня 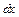, который находится на 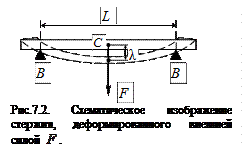расстоянии 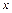от конца стерж 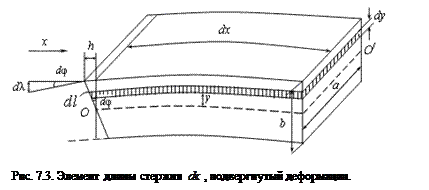ня, поперечное сечение которого характеризуется высотой 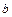и шириной 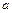(рис. 7.3). Согласно закону Гука, сила 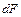, вызывающая удлинение 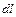произвольно выбранного слоя стержня высотой 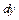, равна:

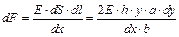, (7.6)

где 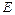– модуль Юнга; 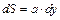– площадь сечения растягиваемого слоя; 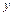– расстояние от нейтрального слоя до слоя высотой 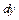, величина:

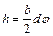(7.7)

определяет положение поперечного сечения стержня до и после деформации, угол 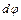является мерой изгиба. При деформации изгиба любое сечение стержня вращается вокруг оси, проходящей через нейтральный слой ОО^/. Тогда общий момент вращения, вызванный упругими силами в поперечном сечении стержня, будет равен:

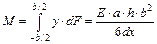. (7.8)

В случае равновесия этот вращающий момент равняется моменту вращения внешней силы:

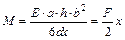, (7.9)

где: 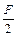– внешняя сила, вызывающая изгиб одного из концов стержня (сила 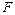распределяется между опорами поровну). Элемент стрелы прогиба 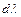может быть представлен (см. рис. 7.3) как:

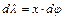. (7.10)

Подставляя величины 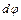и 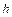из уравнения (11.7), из (11.9) выражаем 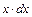и подставляем в (11.10), интегрируя его в пределах от 0 до 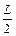, получаем:

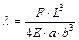, (7.11)

где: 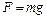. Тогда:

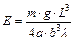. (7.12)

Последнее выражение позволяет рассчитать модуль Юнга, так как все величины доступны для измерения.