Инструментальные средства моделирования систем.

Математическая схема – это абстрактная схема перехода от качественного описания объекта к конкретному формальному виду математического описания.

В общем случае функционирование системы описывается множеством величин:

Входных воздействий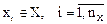

Воздействий внешней среды

Внутренних параметров системы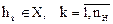

Выходные характеристики системы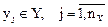

Процесс функционирования в общем виде запишется в виде:

, где F_S – закон функционирования системы.

Полученное соотношение может быть задано различными способами. Например, аналитически, графически, таблично и т.д.

Иногда соотношение получают через свойства системы в конкретные моменты времени, которые называют состояниями. Для описания процесса через состояния используют вектор состояний.

,

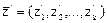где ; ; 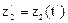…; 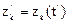в момент времени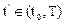

Тогда процесс функционирования запишется в виде:

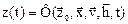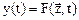и или

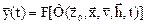
Если не учитываются случайные возмущения внешней среды и изменения внутренних параметров, то мы получаем детерминированную модель в виде:

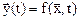
Приведенные соотношения образуют математические схемы общего вида, которые позволяют описать системы в целом, в зависимости от качественных характеристик системы.

Поэтому ввели понятие типовых математических схем, к которым относят: дифференциальные уравнения, конечные и вероятностные автоматы, системы массового обслуживания, сети Петри и т.д.

С помощью типовых математических схем невозможно описать сложные системы, поэтому применяют агрегативное описание системы при котором объект разбивают на конечное число подсистем, сохраняя связи обеспечивающие взаимодействие частей.

Выделяют следующие основные подходы построения моделей процессов: непрерывно-детерминированный (например, дифференциальные уравнения); дискретно-детерминированный (конечные автоматы); дискретно-стохастический (вероятностные автоматы); непрерывно стохастический (системы массового обслуживания); и обобщенный или универсальный (агрегативные системы).

Непрерывно-детерминированные модели (D – схемы)

От латинского dynamic.

Такими моделями описываются системы неподверженные случайным отклонениям внешней среды и внутренних параметров. Обычно описываются дифференциальными уравнениями (обыкновенными, в частных производных и различных порядков).

Основное соотношение для этих моделей запишется в виде:

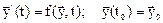
где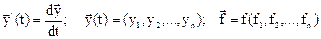

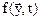- непрерывная вектор функция в (n+1) мерном пространстве.

В основном непрерывно-детерминированные модели применятся в системах автоматического управления.