Принцип относительности и постулаты Эйнштейна
Кроме основных свойств симметрии, рассмотренных в п. 2.2, пространство и время обладают некоторыми более сложными симметриями. Одна из них выражается принципом относительности.
Первым к формулировке принципа относительности подошел Галилей, вошедший в историю культуры своей знаменитой фразой: «А все-таки она вертится!». Галилей имел в виду, что не звездное небо вращается вокруг Земли, а Земля — вокруг своей оси. Католическая церковь, посадив пожилого ученого в темницу, вынудила его отречься от своей точки зрения; однако у Галилея были и оппоненты, предпочитавшие честный спор. Последние говорили: если бы Земля вправду вращалась, то камень, выпущенный из рук, не мог бы падать вертикально вниз, ведь за время его падения та точка Земли, над которой он был уронен, сместилась бы на восток. Поскольку линейная скорость вращения Земли на широте Москвы превышает 280 метров в секунду, то, будь противники Галилея правы, выпущенный из рук камень должен был бы, подобно пуле, врезаться в западную стену помещения. По той же причине следовало бы ожидать постоянного восточного ветра ураганной силы, и т.п.
Галилей придумал мысленный эксперимент, демонстрирующий несправедливость этих возражений и ставший известным как «корабль Галилея». Представим, говорил он, что вы просыпаетесь в трюме корабля и желаете выяснить, стоит ли корабль на якоре или идет под всеми парусами. Как это сделать, не выглядывая наружу? Очевидно, следует провести какой-то эксперимент, который дает разные результаты на стоящем и на плывущем корабле. Попробуем, например, выпустить из руки камень. На стоящем корабле он упадет вертикально вниз. А вот плывущий корабль, если следовать логике оппонентов Галилея, должен за время падения сместиться, и потому путешественник в трюме должен наблюдать отклонение падающего камня от вертикали — в сторону, противоположную движению судна.
На самом деле любой, кто ронял что-либо в поезде, самолете или на корабле, знает, что никакого сноса в сторону, противоположную движению, нет. Галилей объясняет, почему: на плывущем корабле и путешественник, и камень, который он держит в руке, имеют скорость корабля. Когда камень выпускают из рук, он сохраняет эту скорость. В результате в каждый момент полета он находится над одной и той же точкой палубы и упадет именно на нее. Проанализировав еще ряд возможных экспериментов, Галилей пришел к выводу, что, не выходя из трюма, путешественник никогда не сможет определить, плывет ли он, и куда!
Основываясь на мысленном эксперименте «корабль Галилея», можно сформулировать положение, известное как принцип относительности:
Любое явление должно идти совершенно одинаково в любой системе отсчета.
Формулировка простая, но нестрогая.
Во-первых, в такой форме принцип относительности справедлив не для любых систем отсчета, а лишь для инерциальных (п.1.7.6.3). Все они должны двигаться равномерно друг относительно друга. Как только скорость тела, с которым связана система отсчета, изменяется (то есть появляется ускорение), последняя тут же становится неинерциальной. Например, неинерциальна система отсчета, связанная с тормозящим трамваем. По этой причине падающий камень в ней, в отличие от «корабля Галилея», будет отклоняться в сторону кабины вагоновожатого.
Во-вторых, выражение «должно идти совершенно одинаково» недостаточно точно. Точнее сказать: «уравнения, описывающие любое явление, должны быть инвариантны относительно преобразований, описывающих переход от одной системы отсчета к другой».
Преобразования, о которых речь, в классической механике называются преобразованиями Галилея и выглядят элементарно. Первое сводится к утверждению, что время во всех системах отсчета течет одинаково и, в свете ньютоновской концепции Абсолютного времени, само собой разумеется. Второе выражает собой закон сложения скоростей, которым пользуются со второго класса школы. Например: с какой скоростью уменьшается расстояние между поездами, идущими навстречу друг другу со скоростями 40 и 60 км/ч? Ответ очевиден: 40 + 60 = 100 (км/ч.)
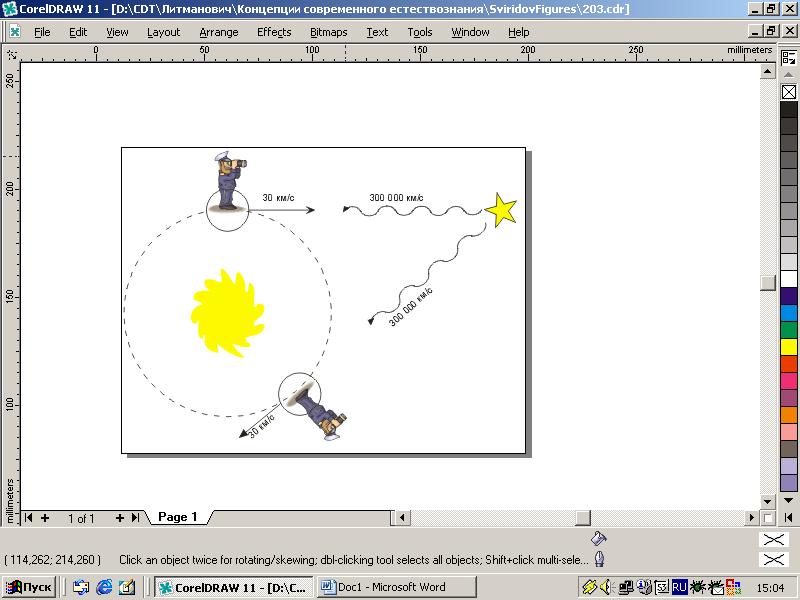
| Рис. 2.3. Идея опытов Майкельсона и Морли |
Уравнения ньютоновской механики оказались действительно инвариантными относительно преобразований Галилея. С электричеством дела обстояли хуже. В середине XIX века Максвелл вывел уравнения, описывавшие все электрические и магнитные явления и с успехом прошедшие
все экспериментальные проверки. Но преобразования Галилея изменяют вид уравнений Максвелла! Что-то было не в порядке либо с первыми, либо со вторыми. В 80-х гг. XIX века Майкельсон и Морли обнаружили, что если скорости движения сравнимы со скоростью света (а свет можно рассматривать как электромагнитную волну), то утрачивают силу преобразования Галилея: нарушается классический закон сложения скоростей.
Идея опытов Майкельсона—Морли заключалась в следующем. Пусть мы наблюдаем с Земли какую-то звезду. Свет от нее летит со скоростью c = 300 000 км/с. Но Земля сама движется вокруг Солнца со средней скоростью 30 км/с. Если проводить наблюдения, когда скорость Земли направлена к звезде, то наблюдатель должен зарегистрировать скорость светового луча 300 000 + 30 = 300 030 км/с («поезда идут навстречу»). Спустя полгода Земля перейдет в противоположную точку своей орбиты и будет удаляться от звезды. Свет звезды будет теперь догонять Землю, а измеренная земным наблюдателем скорость луча должна стать равной 299 970 км/с. Эти изменения слабы, но техника конца XIX века уже позволяла уверенно их регистрировать. Однако из опытов Майкельсона—Морли вытекал поразительный результат: независимо от движения Земли, измеренная скорость света, приходящего от любой звезды, составляет ровно 300 000 км/с, ни больше, ни меньше. Это выглядело так же невероятно, как если бы правильный ответ к школьной задачке о поездах, рассмотренной двумя абзацами выше, был не 100, а 60 км/ч!
Открытие Майкельсона—Морли вызвало большое волнение среди ученых. Сами его авторы в течение 40 лет трижды повторяли измерения, каждый раз повышая их точность на порядок, — с тем же результатом. Появился целый ряд теорий, пытавшихся спасти закон сложения скоростей и объяснить, почему опыт Майкельсона—Морли дает «неправильный» результат. Наиболее последовательная из них принадлежала Хендрику Лоренцу. Он показал: если предположить, что
а) в любом движущемся теле возникают силы, сжимающие его в направлении движения в определенной степени, и
б) все процессы в этом теле в той же степени замедляются,
то ошибка, возникающая благодаря этому в показаниях прибора Майкельсона—Морли, в точности компенсирует измеряемый эффект.
Лоренц очень тщательно разработал математическую сторону своей теории, однако предположения, лежащие в ее основании, выглядели весьма уязвимыми. Оставалось непонятным, что за силы могли бы сжимать движущиеся тела и замедлять течение процессов в них, причем в одной и той же степени, не зависящей от природы тела. Кроме того — и это главное — теория была ущербной с точки зрения научного метода. Основная ее идея заключалась в том, что эффект на самом деле есть, но его принципиально невозможно заметить и измерить. Но если нечто не поддается наблюдению и измерению, то как можно утверждать, что оно существует на самом деле?
Эйнштейн в 1905 г. предложил принципиально иной подход. Эксперимент показывает, что, как бы ни двигался наблюдатель, его приборы неизменно показывают одну и ту же скорость света? Значит, это закон природы! Примем его как постулат (второй постулат Эйнштейна):
В любой системе отсчета скорость света в вакууме
неизменно равна c = 300 000 км/с.
Первый же постулат Эйнштейна — это уже знакомый нам принцип относительности, который удобно сформулировать так:
Все инерциальные системы отсчета совершенно равноправны,
среди них нет выделенных или предпочтительных.
К началу XX века справедливость принципа относительности подтверждалась данными не только механики, но всех разделов физики. Кроме того, он предполагает симметрию, гармоничность окружающего мира. А Эйнштейн был глубоко убежден, что теория, правильно описывающая мир, должна быть красивой.
Задача, поставленная Эйнштейном, заключалась в том, чтобы выяснить, какие выводы следуют из этих двух постулатов. Оказалось, что эти выводы идут вразрез с привычными представлениями о свойствах пространства и времени. Анализ следствий из постулатов Эйнштейна составляет содержание специальной теории относительности (СТО). Представления теории относительности называют релятивистскими (от англ. relativity — относительность).
2.4. Следствия из постулатов Эйнштейна: релятивистский мир
Дата добавления: 2015-01-13; просмотров: 1795;
