Сведения из теории. При соединении трехфазного потребителя по схеме «треугольник» конец потребителя в первой фазе соединяется с началом потребителя во второй фазе (точка b на
При соединении трехфазного потребителя по схеме «треугольник» конец потребителя в первой фазе соединяется с началом потребителя во второй фазе (точка b на рис. 5.1), конец потребителя во второй фазе соединяется с началом потребителя в третьей фазе (точка с) и конец потребителя в третьей фазе соединяется с началом потребителя в первой фазе (точка а). Получается треугольник с вершинами в точках а, b, с.
Необходимо иметь в виду, что схема включения потребителя не зависит от схемы включения источника (генератора). Обмотки генератора (источника) чаще всего включаются по схеме «звезда». Такая схема и ее векторная диаграмма рассмотрены в предыдущей работе, а здесь отметим, что линейные провода соединяют клеммы источника А, В, С с соответствующими клеммами потребителя а, b, с (рисунок 5.1).
На рисунке 5.1 видно, что каждая фаза потребителя присоединяется соответственно к двум линейным проводам.
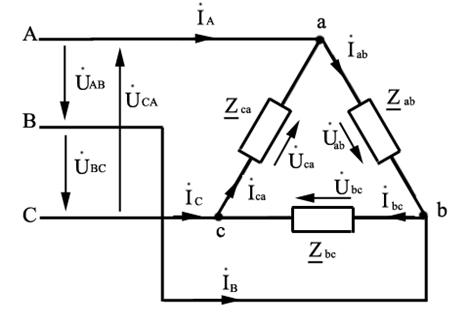
Рисунок 5.1 — Включение потребителей по схеме «треугольник».
Поэтому при соединении потребителей по схеме «треугольник» фазные напряжения равны соответствующим линейным напряжениям:
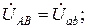
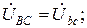
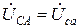 .
.
Фазные токи, которые, как и напряжения, обозначаются двойным индексом, можно определить из закона Ома для участка цепи, а именно:
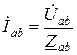 ,
, 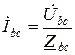 ,
, 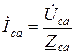 .
.
Отсюда видно, что токи в каждой фазе зависят только от своих линейных напряжений и сопротивлений своих фаз. Следовательно, независимую работу потребителей в такой схеме может обеспечить трехпроводная линия электропередачи. Это является преимуществом схемы «треугольник», т. к. независимую работу потребителей в схеме «звезда» может обеспечить четырехпроводная линия («звезда» с нейтральным проводом). Недостатком схемы «треугольник» является то, что у потребителя будет только одно напряжение — линейное.
На основании первого закона Кирхгофа для узлов а, b, с потребителя можно записать выражения для линейных токов:
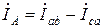 ;
; 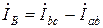 ;
; 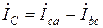 .
.
На схеме (рисунок 5.1) условно принято: все линейные токи ориентированы от источника к потребителю, а все фазные токи — по часовой стрелке.
Допустим, сопротивления фаз разные и чисто активные: Rab ¹ Rbc ¹ Rca, поэтому фазные токи при одинаковых напряжениях будут разными. Векторная диаграмма напряжений и токов показана на рисунке 5.2.
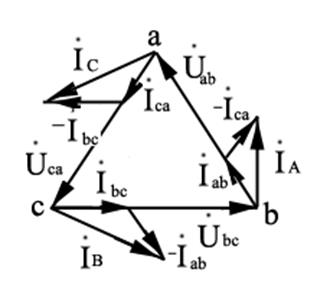
Рисунок 5.2 — Векторная диаграмма напряжений и токов
при соединении потребителя треугольником
Если нагрузка будет симметричной, то треугольники токов становятся равнобедренными с одинаковыми фазными Iab = Ibc = Ica = Iф и равными линейными токами IА = IВ = IС = Iл, откуда следует, что Iл = 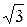 Iф.
Iф.
Обрыв фазы потребителя при соединении треугольником следует рассматривать как выключение потребителя в этой фазе, и это есть частный случай несимметричной нагрузки. При обрыве линейного провода в трехфазной цепи с нагрузкой, включенной треугольником, трехфазная система токов исчезает. Это эквивалентно включению потребителя в однофазную цепь, и на векторной диаграмме треугольники исчезают.
Мощности в трехфазной цепи при соединении потребителей треугольником можно определить по известным формулам, приведенным в предыдущей работе, но токи, напряжения и угол сдвига фаз будут иметь индексы из двух букв.
Активная мощность
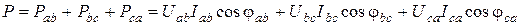 .
.
Реактивная мощность
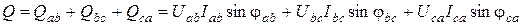 .
.
Полная мощность
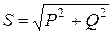 .
.
Фазные мощности (Раb, Pbc, Pca, Qab, Qbc, Qca) при симметричном режиме равны, поэтому в таком случае
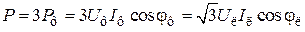 ;
;
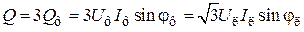 ;
;
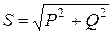
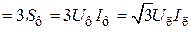 .
.
Дата добавления: 2015-03-03; просмотров: 1359;
