Сведения из теории. Резонанс токов возникает в цепи синусоидального тока при параллельном включении ветвей, содержащих R
Резонанс токов возникает в цепи синусоидального тока при параллельном включении ветвей, содержащих R, L и С (рисунок 3.1). Его можно трактовать как увеличение токов, текущих в ветвях (I1 и I2) по сравнению с током общей цепи I, т. е. при резонансе I1 » I2 и могут быть больше или даже значительно больше I (явление усиления по току).
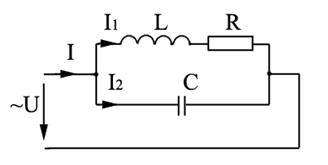
Рисунок 3.1
Исходя из первого закона Кирхгофа,
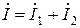 .
.
Для наглядности построим векторную диаграмму токов (рисунок 3.2).
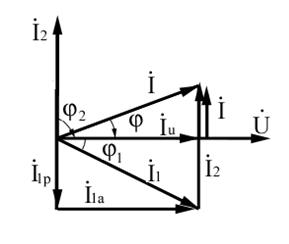
Рисунок 3.2 — Векторная диаграмма токов
Вектор тока İ2 опережает вектор напряжения на 90°, а вектор тока İ1 отстает от вектора напряжения на угол
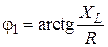 .
.
При резонансе токов необходимо, чтобы
I1 = I1Р= I1sinj1 = I2,
где I1Р — реактивный ток в первой ветви.
Эти токи будут полностью компенсировать друг друга благодаря тому, что имеют разность фаз 180º, общий ток в неразветвленной части цепи совпадает по фазе с напряжением, т. е. становится чисто активным, угол j = 0, cosj = 1.
Аналитический расчет параллельных цепей переменного тока производится с помощью проводимостей. В данном случае общий ток цепи
I = Uy = U 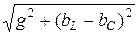 ,
,
где U — напряжение, приложенное к цепи, В;
y — полная проводимость цепи, 1/Ом = См (сименс);
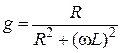 — активная проводимость ветви R, L;
— активная проводимость ветви R, L;
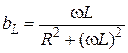 — индуктивная проводимость ветви R, L;
— индуктивная проводимость ветви R, L;
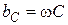 — ёмкостная проводимость ветви с конденсатором.
— ёмкостная проводимость ветви с конденсатором.
Изменяя индуктивность L, ёмкость С, сопротивление R или частоту питающего напряжения, можно добиться того, что  будет равняться
будет равняться 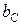 , и тогда общий ток I = Ug становится чисто активным. Это соответствует режиму резонанса. Следовательно, условие резонанса токов можно записать как
, и тогда общий ток I = Ug становится чисто активным. Это соответствует режиму резонанса. Следовательно, условие резонанса токов можно записать как  =
= 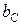 или
или
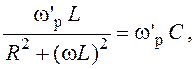
откуда резонансная частота
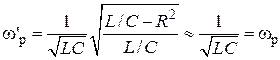 ,
,
где 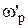 — резонансная частота параллельного контура;
— резонансная частота параллельного контура;
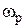 — резонансная частота последовательного контура.
— резонансная частота последовательного контура.
В частном случае, когда можно пренебречь активным сопротивлением катушки индуктивности, условием резонанса становится равенство 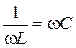 или
или 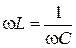 . В этом частном случае ток в неразветвленной части цепи равен нулю. Это значит, что притока энергии извне нет, но в замкнутом контуре, образуемом двумя ветвями, ток проходит. В этом контуре происходит непрерывное превращение энергии электрического поля, запасенного конденсатором, в энергию магнитного поля, запасенную катушкой, и обратно.
. В этом частном случае ток в неразветвленной части цепи равен нулю. Это значит, что притока энергии извне нет, но в замкнутом контуре, образуемом двумя ветвями, ток проходит. В этом контуре происходит непрерывное превращение энергии электрического поля, запасенного конденсатором, в энергию магнитного поля, запасенную катушкой, и обратно.
Для реального контура, обладающего активным сопротивлением R (сопротивление соединительных проводов, активное сопротивление катушки индуктивности 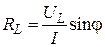 ), протекание тока будет сопровождаться кроме обратимого обмена энергией также необратимым преобразованием электрической энергии в другие виды энергии (тепловую, лучевую, механическую, химическую).
), протекание тока будет сопровождаться кроме обратимого обмена энергией также необратимым преобразованием электрической энергии в другие виды энергии (тепловую, лучевую, механическую, химическую).
С этими процессами напрямую связаны мощности цепи синусоидального тока, так как коэффициент мощности
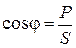 ,
,
где 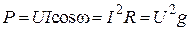 — активная мощность, Вт;
— активная мощность, Вт;
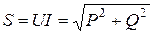 — полная мощность, ВА;
— полная мощность, ВА;
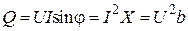 — реактивная мощность, ВАр.
— реактивная мощность, ВАр.
Так как b =  -
- 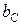 , то
, то 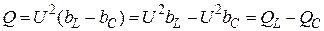 .
.
Наряду с понятием активной мощности Р и реактивной мощности Q применяется понятие полной мощности
S = UI.
Полная, активная и реактивная мощности образуют так называемый треугольник мощностей (рисунок 3.3).

Рисунок 3.3 — Треугольник мощностей
Как видно из треугольника мощностей, при снижении реактивной мощности до нуля полная мощность становится равна активной мощности, угол j уменьшается до нуля.
Для компенсации индуктивной составляющей реактивной мощности QL параллельно нагрузке включают конденсаторы. При этом, подбирая ёмкость конденсатора, можно добиться приближенной компенсации реактивной мощности потребителей электрической энергии, т. е. обеспечить QL- QС ® 0.
Повышение коэффициента мощности cosj используется в электроснабжении.
Большинство потребителей электроэнергии являются активно-индуктивной нагрузкой, что приводит к уменьшению коэффициента мощности. Параллельное подключение конденсатора приводит к уменьшению тока в подводящих проводах при неизменной активной мощности. При этом уменьшаются потери в линиях электропередач, которые пропорциональны квадрату тока:
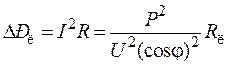 .
.
Аналогично снижаются потери в обмотках генераторов и трансформаторов, снабжающих электростанций и трансформаторных подстанций.
Ёмкость, необходимую для повышения коэффициента мощности до требуемого значения, можно определить по формуле:
С= 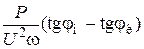 ,
,
где jн, jк — угол сдвига фаз между напряжением и током до компенсации и после компенсации соответственно;
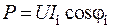 — активная мощность, потребляемая нагрузкой;
— активная мощность, потребляемая нагрузкой;
w=2pf — частота синусоидального тока.
Дата добавления: 2015-03-03; просмотров: 930;
