Введение. Если к концам проводника с активным сопротивлением приложено напряжение, величина которого в каждый момент времени определяется уравнением:
Если к концам проводника с активным сопротивлением 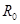 приложено напряжение, величина которого в каждый момент времени
приложено напряжение, величина которого в каждый момент времени 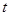 определяется уравнением:
определяется уравнением:
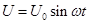 , (1)
, (1)
где 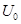 – амплитуда, а
– амплитуда, а 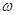 – круговая частота, то в нем возникает электрический ток, сила которого определяется по закону Ома:
– круговая частота, то в нем возникает электрический ток, сила которого определяется по закону Ома:
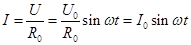 , где
, где 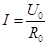 . (2)
. (2)
 Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, то есть напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 1).
Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, то есть напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 1).
Если же помимо сопротивления 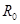 в цепи имеется индуктивность, характеризуемая коэффициентом индуктивности
в цепи имеется индуктивность, характеризуемая коэффициентом индуктивности 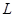 , то под действием того же напряжения возникает ток силой:
, то под действием того же напряжения возникает ток силой:
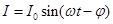 , (3)
, (3)
где 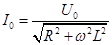 ,
,
 а сдвиг фаз между током и напряжением, определяется из формулы:
а сдвиг фаз между током и напряжением, определяется из формулы:
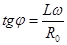 . (4)
. (4)
Из сопоставления уравнений (1) и (3) следует, что в этом случае ток отстаёт по фазе от напряжения (рис. 2).
Величина 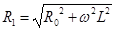 носит название сопротивления, так как она играет в формуле (4) ту же роль, что и обыкновенное сопротивление
носит название сопротивления, так как она играет в формуле (4) ту же роль, что и обыкновенное сопротивление 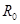 в формуле закона Ома. Величина же
в формуле закона Ома. Величина же 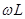 =XL называется индуктивным сопротивлением.
=XL называется индуктивным сопротивлением.
Если вместо индуктивности в цепь переменного тока включена емкость C, то сила тока выражается формулой:
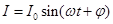 , (5)
, (5)
где 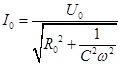 , (6)
, (6)
а 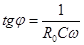 .
.
 В этом случае сила тока опережает по фазе напряжение (рис. 3).
В этом случае сила тока опережает по фазе напряжение (рис. 3).
Сопротивление цепи 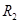 теперь запишется так:
теперь запишется так:
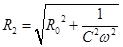 , причем величина
, причем величина 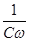 =XC называется емкостным сопротивлением.
=XC называется емкостным сопротивлением.
Наконец в случае, когда в цепь включены последовательно все три величины 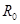 ,
, 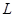 ,
, 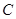 сила тока в цепи может быть записана выражением:
сила тока в цепи может быть записана выражением:
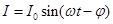 ,
,
где , 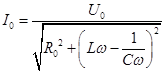 , (7)
, (7)
а 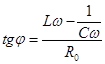 .
.
Полным сопротивлением (его называют импеданс) при этом является:
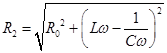 . (8)
. (8)
 Выражение (7) носит название формулы закона Ома для цепи переменного тока.
Выражение (7) носит название формулы закона Ома для цепи переменного тока.
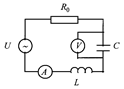
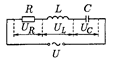
 Цепь с активным сопротивлением, индуктивностью и емкостью представляет собой общий случай последовательного соединения активных и реактивных сопротивлений и является последовательным колебательным контуром (рис. 4).
Цепь с активным сопротивлением, индуктивностью и емкостью представляет собой общий случай последовательного соединения активных и реактивных сопротивлений и является последовательным колебательным контуром (рис. 4).
Вектор результирующего напряжения U замыкает треугольник векторов U, U и U (рис. 4). U+Uс определяет напряжение на индуктивности и емкости. Как видно из диаграммы, это напряжение может быть меньше напряжения на каждом из участков в отдельности. Это объясняется процессами обмена энергией между индуктивностью и емкостью.
Энергетические процессы в данном случае сложнее, чем в ранее рассмотренных простых цепях. Усложнение объясняется тем, что наряду с обменом энергией между генератором и приемником совершается обмен энергией внутри приемника, между катушкой и конденсатором (рис. 5).
Во всех приведенных формулах под 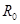 следует подразумевать сумму всех активных сопротивлений цепи (в том числе и катушки индуктивности).
следует подразумевать сумму всех активных сопротивлений цепи (в том числе и катушки индуктивности).
2. Постановка задачи
В данной работе изучают цепь переменного тока. Измеряют активное, индуктивное и емкостное сопротивления цепи, определяют сдвиг фаз между током и напряжением, проверяют закон Ома для цепи переменного тока. Для этого в цепь переменного тока включают последовательно сопротивление 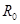 , конденсатор
, конденсатор 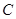 , катушку индуктивности
, катушку индуктивности 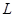 и амперметр A (рис. 6).
и амперметр A (рис. 6).
|

|
Вольтметр V подключают параллельно либо сопротивлению, либо индуктивности, либо конденсатору, либо к части цепи, содержащей сопротивление, конденсатор и катушку индуктивности. Измеряя силу тока и напряжение на соответствующем элементе или участке цепи, определяют соответственно:
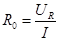 ;
; 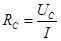 ;
; 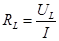 ;
; 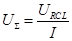 .
.
Затем рассчитывают 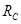 ,
, 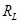 , и
, и 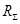 по формулам (
по формулам ( 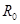 указано на плате):
указано на плате):
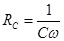 ,
, 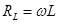 ;
; 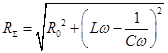 (9)
(9)
и производят сравнение измеренных и рассчитанных величин. Сдвиг фаз определяют по формуле:
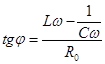 . (10)
. (10)
Дата добавления: 2015-03-03; просмотров: 570;