Паутинообразная модель

Среди этих других подходов, объясняющих механизм установления рыночного равновесия, можно отметить паутинообразную модель, которая (в отличие от ранее рассмотренных) относится к числу динамических, т. е. учитывающих фактор времени. Паутинообразная модель рассматривает процесс формирования равновесия в условиях, когда реакция участников сделок на изменяющиеся условия рынка растянута по времени.

Для примера чаще всего берут различные отрасли сельскохозяйственного производства, например, выращивание птицы. Предположим, наш производитель ориентировался на рыночную цену P_t, по которой птицу продавали в данном году. Естественно, он ожидает сохранения сложившихся цен и определяет объем производства птицы (Q_t) в следующем году исходя из этих цен. Предположим, что рынок вышел из состояния равновесия. Спрос на птицу снизился, и по цене P_t потребители уже не станут покупать столько продукции, сколько раньше. Чтобы реализовать произведенное количество производитель вынужден снижать цену до P₁, т. е. до уровня цены спроса на данное количество птицы (рис. 4.10).

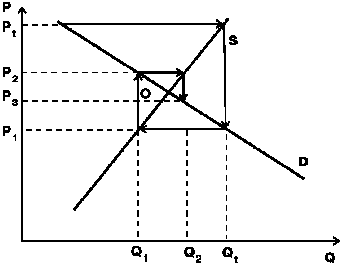
Рис. 4.10. Паутинообразная модель

Но такая низкая цена вынудит какую-то часть производителей покинуть данный рынок. Предложение упадет до Q₁, на рынке возникнет дефицит и, как следствие, будет повышение цен до P₂. Это в свою очередь вызовет расширение предложения, но не до исходного уровня Q_t, а до чуть меньших размеров Q₂. В дальнейшем процесс идет по той же схеме и в конечном итоге, описывая круги сужающейся спирали вокруг точки О, производители «нащупывают» равновесную цену.

В описанном варианте отклонение от равновесия с течением времени уменьшается, т. е. сисМодуль стремится к положению равновесия. Но возможны и иные варианты, представленные на графиках 4.11 (а и б), когда отклонение от равновесия возрастает (рис. 4.11 а) и когда отклонения от равновесия стабильно держатся на одном уровне (рис. 4.11 б).

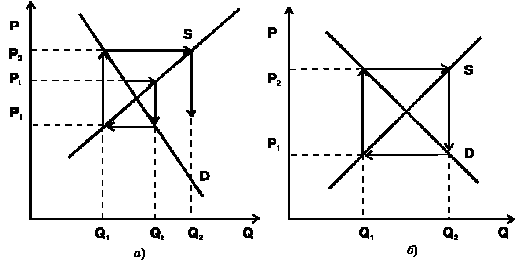
Рис. 4.11. Паутинообразная модель с неустойчивым равновесием

В нашей графической интерпретации возможности достижения рыночного равновесия и его устойчивость определяются углами наклона линий спроса и предложения (их крутизной)⁴. При более крутой кривой предложения и более пологой кривой спроса равновесие устойчиво; в противоположном варианте равновесие неустойчиво ¾ модель «идет вразнос». И наконец регулярные колебания вокруг положения равновесия характерны для ситуации с одинаковым наклоном кривых спроса и предложения.

Примером паутинообразной модели может служить не только рынок сельскохозяйственной продукции. Эта модель применима почти во всех случаях, когда спрос зависит от текущих цен, а предложение реагирует с некоторым временным отставанием. Явления этого типа можно наблюдать, допустим, на биржевом рынке ценных бумаг и валюты: спрос мгновенно реагирует на текущие котировки, а предложение меняется медленнее.

Но бывают на биржах и взрывные колебания ¾ так называемые биржевые паники, когда за считанные минуты ценные бумаги могут резко обесцениться. Новая Россия пережила несколько таких паник, самые острые из них с интервалами в несколько месяцев произошли со второй половины 1997 г. до осени 1998 г. Общим итогом их стало почти десятикратное обесценение акций российских предприятий.

Чтобы во время паники отклонения цен от равновесного уровня не зашли слишком далеко, биржи ¾ в том числе и российские ¾ на время прерывают свои операции. В течение перерыва и сторона спроса, и сторона предложения успевают обдумать ситуацию. Разрыв между ними по времени принятия решений исчезает, и на следующий день паника обычно проходит.

Хотя это, возможно, встревожит наших читателей, паутинообразная модель применима и к рынку дипломированных экономистов. Их предложение, т. е. выпуск вузами, ориентируется на спрос и соответственно на заработную плату, которая была 5 лет назад. Ведь именно тогда нынешние выпускники поступали на первый курс.