Розподіл досліджуваних по групах залежно від «сили» установки
| № групи | Так | Так | Так | Ні | Ні | Ні |
| + | + | + | ||||
| + | + | + | ||||
| + | + | + | ||||
| + | + | + |
У результаті не тільки можна було визначити вираженість певної ознаки (в цьому разі – расових установок), а й упорядкувати класи об’єктів залежно від міри вираженості ознаки (у цьому прикладі перша група мала «найслабкіші» расові установки, а четверта – «найсильніші»).
Мірою центральної тенденції для такого виду шкал є медіана, яка визначається за формулою
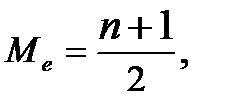
де n – кількість ознак. Ліворуч і праворуч від медіани знаходиться 50 % випадків.
Проблемою, що утруднює маніпуляції з даними, які вимірювалися за ранговою шкалою, є те, що відстань між позначками шкали не відповідає реальній відстані між даними. Крім того, для порівняння даних у різних дослідах (де використовувалися різні експериментальні завдання) за цією шкалою часто необхідно переводити «сирі» первинні дані у спеціальні показники – процентилі, які показують відносне положення індивіда в порівнянні з іншими. Процентильні показники виражаються в одиницях від процентів досліджуваних, результат яких нижче певної первинної оцінки. Чим нижча процентиль, тим гіршою є позиція індивіда в даній групі за вимірюваною якістю.
Наприклад, якщо 35 % людей розв’язують правильно менше 15 експериментальних завдань, то первинна «сира» оцінка – 15 у цьому випадку відповідає 35 процентилю (Р 35). П’ятдесятий процентиль (Р 50) відповідає медіані. Р 25 і Р 75 називають також першим і третім квартилями, оскільки вони позначають нижню і верхню чверть розподілу даних.
У разі переведення «сирих» балів у процентилі вважають, наприклад, що ступінь переваги досліджуваного в досліді X є більш явним, ніж у досліді Y, якщо в X вище його даних виявилося тільки 20 % досліджуваних, у той час як у Y – 40 %. Пряме порівняння оцінок цих двох дослідів не мало б сенсу, оскільки будь-яке числове перетворення на ранговій шкалі може змінювати експериментальний результат.
Третім видом шкал є шкала інтервалів, на якій ознаки не тільки упорядковані за мірою вираженості, а й відстань між позначками шкали відповідає реальному розриву між даними.
Слід зауважити, що установити дослідним шляхом зазначену рівність інтервалів досить важко. Поширеним засобом є статистичне визначення рівності інтервалів через приведення даних порядкової шкали до, як правило, нормального розподілу.
Існують такі підходи до перетворення розподілу в нормальний:
• зміна експериментальних умов виміру (зокрема, характеру поставлених запитань, часу їхнього розв’язання, критеріїв, які визначають позитивні відповіді на кожне з цих запитань), коли, наприклад, емпірично починають змінювати запитання в потрібному напрямі, уникаючи занадто «легких» чи «важких» запитань, за яких більшість відповідей була би помилковою чи правильною; (першим прикладом такого підходу можна вважати шкалу Стенфорда – Біне з визначення інтелекту, коли завдання добиралися таким чином, щоб для кожного віку отримати найтиповіший показник інтелекту 100, із статистичною мірою дисперсії 16);
• нормалізація за складом, при цьому група даних розподіляється на кілька класів таким чином, щоб границі класів відповідали нормальному розподілу;
• нормалізація змінної через її логарифмування:
X = log(х + С),
де С – константа, яка добирається таким чином, щоб наблизити розподіл до нормального, х – первинне значення змінної, X – перетворене значення змінної х;
• нормалізація змінної може також відбуватися через перехід від процентилів до нормалізованих стандартних показників.
Класичним прикладом шкали інтервалів є термометр. Слід зауважити, що шкала інтервалів має одиницю виміру, але положення точки відліку – 0 – є довільним (наприклад, для температурної шкали позначка 0 свідчить не про відсутність температури взагалі, а про певні її значення). Вважається, що на цій шкалі можна виконати певні дії, отримуючи нові показники (X) із старих (х) за допомогою перетворення: X = ах + b, де а і b є константами.
Мірою центральної тенденції на цій шкалі є середнє арифметичне, яке визначається за формулою
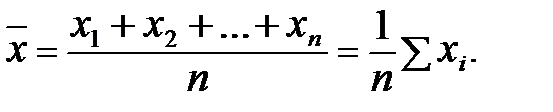
де n – кількість елементів.
Проблемою такого виду шкал є незбіжність природної нульової позначки і нульової позначки на шкалі, що унеможливлює знаходження пропорцій і відношень, наприклад, не можна сказати, що людина з інтелектом 140 є вдвічі розумнішою, ніж людина з інтелектом 70.
Четвертим видом шкал, які у психології, як правило, використовуються як додаткові, є шкали відношень або пропорцій, для яких нульова позначка на шкалі відповідає природній нульовій позначці. На таких шкалах вимірюється довжина, площа, об’єм об’єктів, а також час перебігу певних процесів.
Мірами центральної тенденції для такої шкали є середнє арифметичнеМ або середнє геометричнеG, яке визначається за формулою
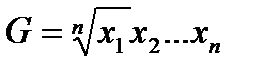
Слід зауважити, що для порівняння результатів двох або більше рядків даних з метою визначення експериментального впливу тільки значень середніх недостатньо. Наприклад, порівняємо дві вибірки зі значеннями:
20; 20; 20; 20 і 38; 2; 38; 2.
Очевидно, середнє арифметичне для них обох дорівнює 20 і не менш очевидно, що це різні вибірки. Тут необхідно, окрім середніх, також визначити дисперсію значень навколо середніх, яке дає більш точну картину, зокрема, середнє квадратичне відхилення, яке обчислюється за формулою
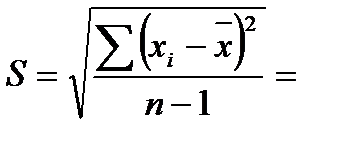
Зазначимо, що чим складніший рівень психіки, тим менш точно його можна виміряти (див. табл. 2)
Таблиця 2
Дата добавления: 2015-02-28; просмотров: 1316;
