Интеллектуальные системы, основанные на нечеткой логике

Описанные выше положения можно применять для логического вывода утвер­ждений. Например, если известно, что х Î А и А Í В, то из аксиомы вывода имеем х ÎВ. Пусть А - множество всех народных депутатов, а В - множество тех, кто пользуется правом бесплатного проезда в общественном транспорте. Тогда утвер­ждение о вхождении А в В трансформируется в правило вывода: "Если лицо явля­ется народным депутатом, то оно пользуется правом бесплатного проезда в обще­ственном транспорте". Если множества не сравнимы непосредственно, может по­требоваться дополнительное функциональное преобразование, которое позволит рассматривать одно множество как подмножество другого. Например, результатом преобразования посылки "температура в комнате 30° С" для кондиционера может служить указание "включить вентилятор". Все значения температур, при которых необходимо его включение, образуют подмножество во множестве условий, при­водящих к включению вентилятора. Преобразование производится функцией уп­равления, роль которой в данном случае может выполнять термостат.

Нечеткое правило логического вывода представляет собой упорядоченную пару (А, В), где А - нечеткое подмножество пространства входных значений X, В - нечеткое подмножество пространства выходных значений Y. Система нечетко­го вывода - это отображение I^разм(X) в I^разм(Y) разм(Z) - оператор определения размерности пространства Z. Число элементов в I^разм(X) в I^разм(Y) бесконечно вели­ко, поэтому невозможно задать правила нечеткого вывода соответствующими парами точек. Однако они могут быть описаны в терминах теории нечетких мно­жеств. Например, вполне работоспособная система кондиционирования может быть описана правилами: "если температура в комнате высокая, то скорость вра­щения вентилятора высокая" и "если температура в комнате низкая, то скорость вращения вентилятора низкая". Подобные правила вывода используются в не­четких экспертных системах. Как правило, они имеют вид: если цена великаи спрос низкий, то оборот мал, где цена и спрос - входные переменные; оборот - выходное значение; вели­ка, низкийимал - функции принадлежности (нечеткие множества), опреде­ленные на множествах значений цены, спроса и оборота соответственно.

Нечеткие правила вывода образуют базу правил. Важно то, что в нечеткой экспертной системе в отличие от традиционной работают все правила одно­временно, но степень их влияния на выход может быть различной. Принцип вычисления суперпозиции многих влияний на окончательный результат лежит в основе нечетких экспертных систем.

Процесс обработки нечетких правил вывода в экспертной системе состоит из четырех этапов:

1. вычисление степени истинности левых частей правил (между "если" и "то") - определение степени принадлежности входных значений нечет­ким подмножествам, указанным в левой части правил вывода;

2. модификация нечетких подмножеств, указанных в правой части правил вывода (после "то"), в соответствии со значениями истинности, получен­ными на первом этапе;

3. объединение (суперпозиция) модифицированных подмножеств;

4. скаляризация результата суперпозиции - переход от нечетких подмно­жеств к скалярным значениям.

Для определения степени истинности левой части каждого правила нечет­кая экспертная система вычисляет значения функций принадлежности нечет­ких подмножеств от соответствующих значений входных переменных. Напри­мер, для правила (1) определяется степень вхождения конкретного значения переменной цена в нечеткое подмножество велика, то есть истинность преди­ката "цена велика". К вычисленным значениям истинности могут применяться логические операции. Наиболее часто используются следующие определения операций нечеткой логики:

truth(НЕ х) = 1 - truth(x),

truth(x И у) = min {truth(x), truth(y)},

truth(x ИЛИ у) = max{truth(x), truth(y)},

где х и у - высказывания; truth(z) - степень истинности высказывания г. Полученное значение истинности используется для модификации нечеткого множества, указанного в правой части правила. Для выполнения такой моди­фикации используют один из двух методов: "минимума" (correlation-min encoding) и "произведения" (correlation-product encoding). Первый метод огра­ничивает функцию принадлежности для множества, указанного в правой части правила, значением истинности левой части (рисунок 4).

Рисунок 4 - Метод "минимума"

Во втором методе значение истинности левой части используется как коэффи­циент, на который умножаются значения функции принадлежности (рисунок 5).

Рисунок 5 - Метод "произведения"

Результат выполнения правила - нечеткое множество. Говоря более строго, происходит ассоциирование переменной и функции принадлежности, указан­ных в правой части.

Выходы всех правил вычисляются нечеткой экспертной системой отдель­но, однако в правой части нескольких из них может быть указана одна и та же нечеткая переменная. Как было сказано выше, при определении обобщенного результата необходимо учитывать все правила. Для этого система производит суперпозицию нечетких множеств, связанных с каждой из таких переменных. Эта операция называется нечетким объединением правил вывода. Например, правая часть правил

если цена мала, то спрос велик

если цена велика, то спрос мал

содержит одну и ту же переменную - спрос. Два нечетких подмножества, получа­емые при выполнении этих правил, должны быть объединены экспертной системой.

Традиционно суперпозиция функций принадлежности нечетких множеств m_1F(x),m_2F(x),…,m_nF(x) определяется как:

m_sumF(x)=max{m_iF(x)} x,iÏ[1,n].

Графическое представление подобной суперпозиции приведено на рисунок 6.

Рисунок 6 - Метод "Max Combination"

Другой метод суперпозиции состоит в суммировании значений всех функ­ций принадлежности (графическая интерпретация приведена на рисунке 7):

.

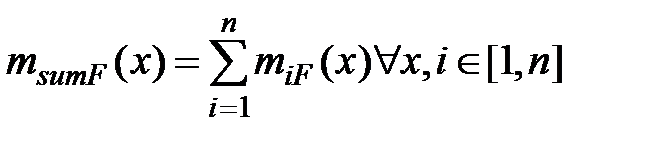Рис. 7. Метод "Sum Combination"

Самым простым (но наименее часто используемым) является подход, когда суперпозиция не производится. Выбирается одно из правил вывода, результат которого используется в качестве интегрального результата.

Конечный этап обработки базы правил вывода – переход от нечетких значений к конкретным скалярным. Процесс преобразования нечеткого множества в единственное значение называется "скаляризацией" или "дефазификацией" (defuzzification).Чаще всего в качестве такого значения используется "центр тяжести" функции принадлежности нечеткого множества (centroid defuzzification method) (рисунок 8).

Рис. 8. Скаляризация методом "центра тяжести"

Другой распространенный подход - использование максимального значе­ния функции принадлежности (modal defuzzification method) (рисунок 9). Кон­кретный выбор методов суперпозиции и скаляризации осуществляется в зави­симости от желаемого поведения нечеткой экспертной системы.

Рис. 9. Скаляризация методом "максимума"

Рассмотрим пример того, как обрабатываются нечеткие правила вывода в экспертной системе, управляющей вентилятором комнатного кондиционера. Задача кондиционера - поддерживать оптимальную температуру воздуха в ком­нате, охлаждая его, когда жарко, и нагревая, когда холодно. Пусть, изменяя ско­рость вращения вентилятора, прогоняющего воздух через охлаждающий эле­мент, мы можем менять температуру воздуха, тогда алгоритм работы кондици­онера может быть задан следующими правилами:

1) если температура воздуха в комнате высокая, то скорость вращения вен­тилятора высокая;

2) если температура воздуха в комнате средняя, то скорость вращения вен­тилятора средняя;

3) если температура воздуха в комнате низкая, то скорость вращения венти­лятора низкая;

Для того чтобы система могла обрабатывать эти правила, надо задать функции принадлежности для нечетких подмножеств, определенных на значениях температу­ры (t) и скорости вращения вентилятора (у). Пусть температура воздуха в комнате на­ходится в пределах от 0°С до 60°С - в противном случае кондиционер вряд ли поможет. Функцию принадлежности для нечеткого подмножества низкая, определенную на интервале изменения температуры, можно задать, например, так (рисунок 10):

Рисунок 10 – Нечеткое подмножество "низкая", определенное на множестве значений температуры

Если температура меньше 12°С, то это - определенно низкая температура для комнаты (m_{Тнизкая}(t)=1,t 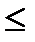12). Температуру выше 20°С никак нельзя на­звать низкой (m_{Тнизкая}(t)=0,t 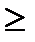20). В промежутке между этими значениями функция принадлежности линейно убывает - с увеличением температуры уменьшается истинность утверждения "температура воздуха в комнате низкая". Аналитически m_{Тнизкая}(t) выражается следующим образом:

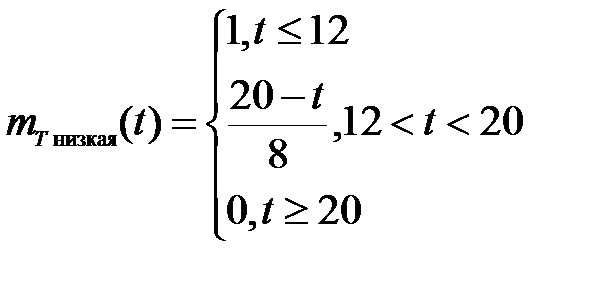
Сходные рассуждения позволяют нам задать функции принадлежности для оставшихся подмножеств: средняяи высокая (рисунок 11-12).

Рисунок 11 ­– Нечеткое подмножество "средняя", определенное на множестве значений температуры

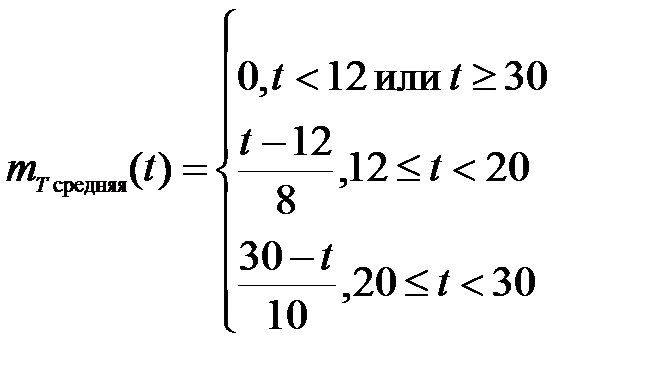
Рисунок 12 – Нечеткое подмножество "высокая", определенное на множестве значений температуры

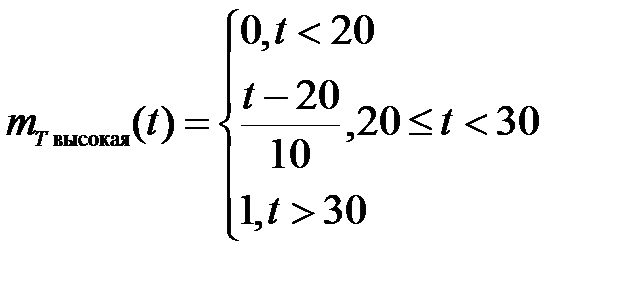
Определим нечеткие подмножества для скорости вращения вентилятора. Пусть она может изменяться от 0 до 1000 об/мин. Вполне допустимым будет следующий вариант определения функций принадлежности для нечетких под­множеств низкая, средняяивысокая (рисунок 13-15).

Рисунок 13 – Нечеткое подмножество "низкая", определенное на множестве значений скорости вращения вентилятора

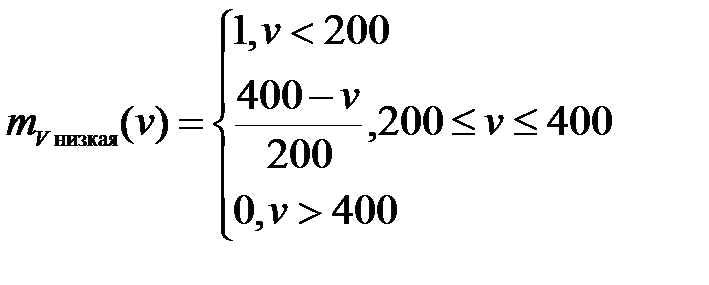
Рисунок 14 – Нечеткое подмножество "средняя", определенное на множестве значений скорости вращения вентилятора

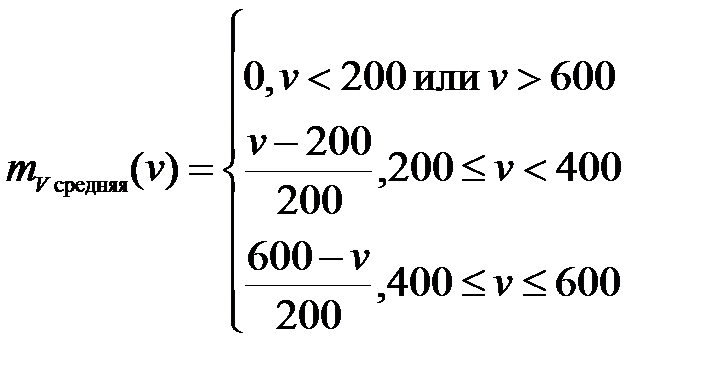
Рисунок 15 – Нечеткое подмножество "высокая", определенное на множестве значений скорости вращения вентилятора

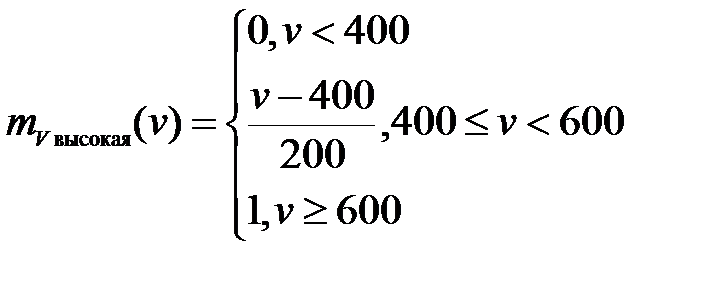
Рассмотрим теперь, как нечеткая экспертная система определяет скорость вращения вентилятора в зависимости от температуры воздуха в комнате. Пусть эта температура равна 22°С.

Сначала экспертной системе надо определить истинность левых частей правил вывода при подстановке в них текущего значения температуры. Для этого она должна найти степень вхождения t = 22°С в каждое из указанных слева нечетких подмножеств. В левых частях правил указаны три подмноже­ства, заданных на интервале значений температуры: высокая, низкая и сред­няя. Степень вхождения находим, вычисляя значение функций принадлежнос­ти каждого из подмножеств от t = 22°С:

m_{Tвысокая}(22)=0.2;

m_{Тсредняя}(22)=0.8;

m_{Тнизкая}(22)=0.

Значения истинности левой части каждого правила используются для мо­дификации нечеткого множества, указанного в его правой части. Модифика­цию будем производить описанным выше методом "произведения",(correlation product encoding). На рис. 9.16 изображено, как трансформируются находящи­еся в правых частях правил нечеткие подмножества высокая, средняя и низкая.

Рисунок 16 – Модификация нечетких подмножеств, определенных на интервале изменения скорости вращения вентилятора

Далее нечеткой экспертной системе необходимо обобщить результаты дей­ствия всех правил вывода, то есть произвести суперпозицию полученных не­четких множеств. Воспользуемся для этого методом "Max Combination" (рисунок 6). Результат объединения нечетких множеств показан на рисунке 17.

Теперь необходимо осуществить переход от суперпозиции множеств к ска­лярному значению. Скаляризацию произведем методом "центра тяжести". Ил­люстрация того, как получается результат, представлена на рисунке 18.

Рисунок 18. Получение скалярного значения скорости вращения вентилятора методом "центра тяжести" для t = 22° С

Центр тяжести фигуры на рисунке 18 находится в точке v=560.5691. Это и будет значением скорости вращения вентилятора, которое выдаст экспертная система при температуре воздуха в комнате равной 22°С. При других значени­ях температуры функция принадлежности обобщенного результата выполне­ния всех правил, изображенная на рисунке 18, будет меняться. Вот как она будет выглядеть, если на вход экспертной системы поступит значение t = 28°С (рисунок 19). Центр тяжести в этом случае находится в точке v=746.6667, поэто­му управляемый нашей системой вентилятор будет вращаться с такой скорос­тью, когда в комнате 28°С.

Рисунок 19 – Получение скалярного значения скорости вращения вентилятора методом "центра тяжести" для t = 28°С

Описанные выше операции выполняются каждый раз, когда требуется ре­зультат логического вывода. В системах, управляющих динамическими про­цессами, эта последовательность действий выполняется циклически. В силу того, что результаты правил вычисляются раздельно, нечеткие экспертные сис­темы эффективно реализуются на базе параллельных вычислительных систем.

Возникает вопрос, оправдана ли настолько сложная система при управле­нии таким простым устройством, как вентилятор? Практика показывает, что оправдана. Так, например, кондиционеры, основанные на нечеткой логике, обес­печивают меньшие, по сравнению с традиционными, колебания температуры. Также они дают существенную экономию электроэнергии. Далее, используя один из пакетов нечеткой логики, мы увидим, как экспертная система, осно­ванная на приведенных выше правилах, функционирует в динамике. Также мы сравним ее работу с обычной схемой управления на базе термостата, использу­ющейся в большинстве устройств охлаждения.

Контрольные вопросы

1. Дайте определение неточных знаний.

2. Что такое нечеткий вывод знаний?

3. Дайте определение понятия Немонотонность вывода.

4. Опишите основные принципы Основы нечеткой логики .

5. Приведите примеры иИнтеллектуальные системы, основанные на нечеткой логике