Вопрос 18: Поляризация света при отражении и преломлении вторичных волн. Принцип Гюйгенса.

При падении естественного света на границу раздела двух изотропных диэлектриков часть его отражается, а часть преломляется и распространяется во второй среде. Установлено, что отраженный и преломленный лучи частично поляризованы: при вращении анализатора вокруг лучей интенсивность света периодически усиливается и ослабевает (полного гашения не наблюдается!). Эти опыты впервые проведены Малюсом (1810). Дальнейшие исследования показали, что в отраженном луче преобладают колебания, перпендикулярные плоскости падения (на рис. 34 обозначены точками), в преломленном – колебания, параллельные плоскости падения (на рис. изображены стрелками).

Степень поляризации отраженного и преломленного света зависит от угла падения естественного света на границу раздела изотропных диэлектриков и показателя преломления. Брюстер (1815) установил закон, согласно которому при угле падения i_B (угол Брюстера), определяемым соотношением 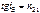(n₂₁ – показатель преломления второй среды относительно первой), отраженный луч является плоскополяризованным(содержит только колебания, перпендикулярные плоскости падения) (рис. 35). Преломленный же луч при угле падения i_B поляризуется частично.

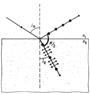Если свет падает на границу раздела под углом Брюстера, то отраженный и преломленный лучи взаимно перпендикулярны. 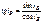, 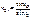(i₂ – угол преломления), откуда cos i_B = sin i₂. Следовательно, i_B + i₂ = π/2, но

i'_B = i_B (закон отражения), поэтому i'_B + i₂ = π/2.

Степень поляризации преломленного света может быть значительно повышена путем многократного преломления при условии падения света каждый раз на границу раздела под углом Брюстера. Если, например, для стекла (п =1,53) степень поляризации преломленного луча составляет ≈ 15%, то после преломления на 8 – 10 установленных подряд стеклянных пластинах вышедший из такой системы свет будет практически полностью поляризованным. Такая совокупность пластинок называется стопой Столетова.